Welcome to booknu's Blog!
PS & Algorithm 공부, 테크 리뷰-
소프트웨어 마에스트로(SWM) 10기 합격 후기
2월달에 시작된 소프트웨어 마에스트로 10기 선발이 끝났다.
처음에는 그냥 지원이나 해보자는 마인드였는데 단계가 지날수록 희망이 보이고, 진짜 해보고 싶다는 마인드가 강해져서 좋은 경험이었다.
자기소개서
9기 선발 때는 자신이 한 프로젝트 설명과 깃허브 링크 같은 것을 요구했다는데, 이번 10기에는 자신의 경험, SWM에 합격에서 무엇을 어떻게 할건지를 물어보는 일반적인 자기소개서 형식이었다.
실제 협업 경험도 없고, 해본 프로젝트라곤 Java로 만든 멀티스레드 다운로더, JSP로 만든 매우매우 조잡한 NAS(개인적인 컴퓨터 - 모바일 파일 공유용) 등 간단한 프로젝트들 밖에 없어서 고민을 많이 했었다.
현재 내가 가진 강점은 알고리즘, PS 밖에 없는데 그마저도 오프라인 대회 본선 진출, 수상 경험도 없고 코드포스 퍼플이라는 굉장히 애매한 것 밖에 없었지만 그래도 그것을 달성하기 위해 했던 노력, 왜 알고리즘을 위주로 공부했는지 등을 썼다.
내가 하고 싶은 프로젝트로는 머신러닝을 이용한 프로젝트를 하고 싶다고 적었는데, 이것이 나중에 있을 면접에 큰 복병이 되었다.
인적성 검사
인적성 검사는 인터넷으로 AI를 이용해서 진행되었다.
나는 군입대 전 신체검사 때 하는 체크 문항으로 된 지능 검사, 사회 적응력 검사 같은 걸 예상하고 가벼운 마음으로 봤는데, 예상 외로 대화 형태, IQ테스트 처럼 진행되서 당황스러웠다.
이런 인적성 검사가 AI로 진행 된다는게 신기했고 한편으로는 기계에게 테스트를 당하는 것 같아 기분이 미묘했다.
특히 벽을 보고 대화하는 것 마냥 인공지능하고 대화를 하는게 고역이었고, IQ테스트도 생각 외로 어려워서 새로운 경험이었다.
코딩 테스트
BOJ나 Codeforces와 비슷한 방식으로 알고리즘 문제를 풀면 되는 테스트였다.
오프라인으로 진행되었으며, 9기 때는 굉장히 쉬운 문제만 나왔다는데, 이번 10기 때는 90분에 15문제를 푸는 형태로 진행되었다.
이 정보를 사전에 알려주었는데, 나는 90분에 15문제이면 어지간히 쉬운 문제들만 내나보다 하고 가벼운 마음으로 코딩 테스트를 보러 갔는데, 높은 배점의 문제는 예상 외로 어려웠고, 제출을 1번 밖에 못해서 제출 시 오답이면 그대로 그 문제를 버려야 했다.
이게 잔인했던게 제출 후 오답 여부를 알려주지 않으면 모르겠는데 바로바로 채점이 되니까 쉬운 문제를 틀려도 멘탈이 깨지고 어려운 문제를 열심히 구현했는데 틀리면 더욱더 멘탈이 깨졌다.
게다가 인텔리센스도 지원하지 않고, 복붙도 안 되는 모두의 코딩 플랫폼 안에서만 코딩을 해야해서 많이 불편했다.
총 10문제에 대해서 제출을 했는데 그 중 3문제가 틀렸고 대부분이 높은 배점에서 틀렸다.
변명이지만 그 날 컨디션이 별로 안 좋았고 예상 외로 높은 난이도에 당황해서 평정심을 잃고 문제를 풀어 별로 좋지 않은 성적을 받은 것 같다.
면접
사실 서류 통과만 된다면 어찌저찌 면접 까지는 거의 무조건 올 것 같다고 생각했다.
코딩 테스트야 내가 가장 노력을 했던 분야이고, 인적성 검사는 심리 테스트 급으로 생각해서 그렇게 생각을 했었는데, 가장 걱정했던 것이 이 면접이다.
과연 면접관들이 기술적으로 파고드는 질문을 많이 할 것인가, 아니면 비전을 물어보고 경험에 대한 질문을 많이 할 것인가가 가장 궁금했었다.
결과적으로, 면접 초반부에는 기술적인 부분들을 많이 질문했고, 후반부에 비전과 경험에 대해 물어보는 방식으로 진행됐다.
하필 내가 속한 면접 조가 1명을 제외하고 모두가 딥러닝, 머신러닝 프로젝트를 하겠다고 했던 터라 초반부터 그와 관련된 기술적인 질문을 엄청나게 많이 받았다.
나는 아직 머신러닝 공부를 시작한지 1달 밖에 안 되었는데 이런 질문들이 쏟아지자 거의 멘탈을 놓은 듯이 횡설수설 했다.
다행히 머신러닝 관련 질문들이 끝나고 내가 대답할만한 질문들이 주어졌을 때는 멘탈을 잡고 대답을 했지만, 면접을 망쳤다고 생각했다.
그나마 플러스 요소가 됐을 것 같은 질문이 “면접관들이 하지 않은 질문 중 자기는 이런 질문을 하면 자신에 대해 어필을 잘 할 수 있을 것 같은데 안 해줘서 아쉬운 질문이 있나요?” 였는데, 나는 여기에 즉시 “나는 남들보다 머신러닝 관련 지식도 현저히 적고 실제 프로젝트 경험도 적지만, 논리적인 사고력을 기르고 문제해결 능력을 키우기 위해 PS를 위주로 공부했는데 너무 머신러닝, 실제 협업 경험에 대해서만 물어봐서 아쉽다” 라고 대답했다.
덕분에 내가 가진 강점에 대해서 어필은 할 수 있었기에 당시에 이 질문을 한 면접관님이 정말 고마웠다.
어찌됐건 30~40분 정도 진행 된 면접에서 멘탈이 탈탈 털리고 멍한 상태로 집을 돌아와서 SW 마에스트로에 대해서는 거의 포기했는데, 합격 소식을 듣고 매우 기뻤다.
(9기까지는 100명의 지원자를 뽑았는데, 10기에서는 150명을 뽑고 이전보다 선발 소식이 별로 안 퍼져 조금 운 좋게 뽑힌 것 같기도 하다.)
후기
선발 과정에 참가하면서 가장 불만이었던 점이 오프라인 코딩 테스트나 면접을 평일에 봐서 대학교 수업을 자주 빠져야 했다는 것이다.
게다가 선발 후 일정도 모두 평일에 진행되는데, 하필 바로 다음 일정이 4월 29, 30일인데 그 날이 전공 시험이 있는 날이라 이걸 어떻게 처리해야 할 지 벌써부터 골치가 아프다.
하지만 SW 마에스트로에 선발 돼서 내가 부족했던 프로젝트 경험과 협업 경험을 쌓을 수 있을 것 같아서 너무 좋다.
이번 학기에 웹 프론트엔드 프로젝트라도 해보려고 멋쟁이 사자처럼 동아리에도 지원했는데 떨어져서 붕 뜬 느낌이었는데, 제대로 프로젝트를 진행해 볼 기회가 생겨서 좋다.
이번 기회에 머신러닝과 프로젝트 경험을 확실히 쌓아가야겠다.
-
코드포스 Codeforces Round #542(Div.2) 리뷰
개요
전반적으로 난이도가 쉬웠다고 생각한다. E번 마저도 입맛대로 결과를 출력해도 돼서 큰 어려움은 없었다.
A번
A번 문제:
그리디$n$개의 원소를 가진 배열이 주어지고, 각 배열의 원소를 $0$이 아닌 $[-1000..1000]$사이의 정수 $d$로 나누었을 때 양수(꼭 정수가 아니어도 됨.)의 개수가 $\lceil \frac{n}{2} \rceil$개가 되는 $d$ 중 아무거나 출력하면 된다.
만약 그런 $d$가 없다면 $0$을 출력한다.
풀이 보기
만약 해당되는 $d$가 존재한다면 $d$는 $-1$ 혹은 $1$일 것이다.
즉, 배열에 양수가 $\lceil \frac{n}{2} \rceil$보다 많다면 $d = 1$이고, 음수가 많다면 $d = -1$이다.
만약 두 경우 모두 존재하지 않으면 $0$이다.
소스코드 보기
#include <bits/stdc++.h> using namespace std; #ifdef LOCAL_BOOKNU #define debug(...) cerr << "[" << #__VA_ARGS__ << "]:", debug_out(__VA_ARGS__) #else #define debug(...) 42 #endif // ........................macro.......................... // #define FOR(i, f, n) for(int (i) = (f); (i) < (int)(n); ++(i)) #define RFOR(i, f, n) for(int (i) = (f); (i) >= (int)(n); --(i)) #define pb push_back #define emb emplace_back #define fi first #define se second #define ENDL '\n' #define sz(A) (int)(A).size() #define ALL(A) A.begin(), A.end() #define UNIQUE(c) (c).resize(unique(ALL(c)) - (c).begin()) #define next next9876 #define prev prev1234 typedef pair<int, int> ii; typedef pair<int, ii> iii; typedef vector<int> vi; typedef vector<vi> vvi; typedef vector<ii> vii; typedef vector<vii> vvii; typedef long long i64; typedef unsigned long long ui64; // inline i64 GCD(i64 a, i64 b) { if(b == 0) return a; return GCD(b, a % b); } inline int getidx(const vi& ar, int x) { return lower_bound(ALL(ar), x) - ar.begin(); } // 좌표 압축에 사용: 정렬된 ar에서 x의 idx를 찾음 inline i64 GCD(i64 a, i64 b) { i64 n; if(a < b) swap(a, b); while(b != 0) { n = a % b; a = b; b = n; } return a; } inline i64 LCM(i64 a, i64 b) { if(a == 0 || b == 0) return GCD(a, b); return a / GCD(a, b) * b; } inline i64 CEIL(i64 n, i64 d) { return n / d + (i64)(n % d != 0); } // 음수일 때 이상하게 작동할 수 있음. inline i64 ROUND(i64 n, i64 d) { return n / d + (i64)((n % d) * 2 >= d); } const i64 MOD = 1e9+7; inline i64 POW(i64 a, i64 n) { assert(0 <= n); i64 ret; for(ret = 1; n; a = a*a%MOD, n /= 2) { if(n%2) ret = ret*a%MOD; } return ret; } template <class T> ostream& operator<<(ostream& os, vector<T> v) { os << "["; int cnt = 0; for(auto vv : v) { os << vv; if(++cnt < v.size()) os << ","; } return os << "]"; } template <class T> ostream& operator<<(ostream& os, set<T> v) { os << "["; int cnt = 0; for(auto vv : v) { os << vv; if(++cnt < v.size()) os << ","; } return os << "]"; } template <class L, class R> ostream& operator<<(ostream& os, pair<L, R> p) { return os << "(" << p.fi << "," << p.se << ")"; } void debug_out() { cerr << endl; } template <typename Head, typename... Tail> void debug_out(Head H, Tail... T) { cerr << " " << H, debug_out(T...); } // ....................................................... // const int MAXN = 100; int n, ar[MAXN]; void input() { cin >> n; FOR(i, 0, n) cin >> ar[i]; } int solve() { int h = n/2 + n%2, cnt = 0, cc = 0;; FOR(i, 0, n) { if(ar[i] > 0) { ++cnt; } if(ar[i] < 0) { ++cc; } } if(cnt >= h) cout << 1 << ENDL; else if(cc >= h) cout << -1 << ENDL; else cout << 0 << ENDL; return 0; } // ................. main .................. // void execute() { input(), solve(); } int main(void) { #ifdef LOCAL_BOOKNU freopen("input.txt", "r", stdin); // freopen("out.txt", "w", stdout); #endif cin.tie(0), ios_base::sync_with_stdio(false); execute(); return 0; } // ......................................... //후기
$d$가 음수도 될 수 있는지 몰라서 양수만 체크했다가 틀렸다.
다시 음수도 체크했는데, 실수로 두 가지 경우 모두 $1$로 출력해서 또 틀렸다.
이것 때문에 많은 시간과 점수를 날려먹었다.
B번
B번 문제:
DP그리디두 사람이 각각 $n$층의 케이크를 만들려고 하고 있다.
각 케이크는 점점 아래층이 커지는 구조로 쌓여야 한다. (어찌 됐던 결국 $[1..n]$순서로 층을 쌓아야 한다.)
$2 \cdot n$개의 케이크 가게가 있는데, 각 케이크 가게는 $[1..n]$층 중 하나를 팔고 있으며, 모든 케이크 가게에서 각 케이크 층은 딱 2번씩 등장한다.
두 사람은 모두 가장 왼쪽에서 재료 모으기를 시작하고, 케이크 가게 사이의 거리는 $1$일 때, 두 사람 모두 케이크를 완성하기 위해 움직여야 하는 움직임의 수의 합의 최소값을 구해야 한다.
풀이 보기
DP 풀이
$dp[i][j]$ = 두 사람이 케이크의 $i$층까지 완성했고, 그 중 첫 번째 사람이 두 케이크 집 중 $j$에 방문중인 상태일 때 최소값
이 때 $j \oplus 1$의 의미는 $j$와 다른 것을 의미한다.
그리디 풀이
위의 DP풀이를 자세히 보면, 결국 이전 상태에서 그리디한 선택만을 가져간다는 것을 알 수 있다.
즉, 이전 상태의 두 케이크 집에서 갈 현재 상태의 두 케이크 집을 거리의 합이 작은 쪽으로 골라서 간다는 것이다.
어찌됐든 두 명 모두 $n$층의 케이크를 완성해야 하고, 현재 있는 집의 위치는 어차피 각각 둘 중 하나이니까 이렇게 그리디하게 생각해도 된다.
소스코드 보기 (DP)
include <bits/stdc++.h> using namespace std; #ifdef LOCAL_BOOKNU #define debug(...) cerr << "[" << #__VA_ARGS__ << "]:", debug_out(__VA_ARGS__) #else #define debug(...) 42 #endif // ........................macro.......................... // #define FOR(i, f, n) for(int (i) = (f); (i) < (int)(n); ++(i)) #define RFOR(i, f, n) for(int (i) = (f); (i) >= (int)(n); --(i)) #define pb push_back #define emb emplace_back #define fi first #define se second #define ENDL '\n' #define sz(A) (int)(A).size() #define ALL(A) A.begin(), A.end() #define UNIQUE(c) (c).resize(unique(ALL(c)) - (c).begin()) #define next next9876 #define prev prev1234 typedef pair<int, int> ii; typedef pair<int, ii> iii; typedef vector<int> vi; typedef vector<vi> vvi; typedef vector<ii> vii; typedef vector<vii> vvii; typedef long long i64; typedef unsigned long long ui64; // inline i64 GCD(i64 a, i64 b) { if(b == 0) return a; return GCD(b, a % b); } inline int getidx(const vi& ar, int x) { return lower_bound(ALL(ar), x) - ar.begin(); } // 좌표 압축에 사용: 정렬된 ar에서 x의 idx를 찾음 inline i64 GCD(i64 a, i64 b) { i64 n; if(a < b) swap(a, b); while(b != 0) { n = a % b; a = b; b = n; } return a; } inline i64 LCM(i64 a, i64 b) { if(a == 0 || b == 0) return GCD(a, b); return a / GCD(a, b) * b; } inline i64 CEIL(i64 n, i64 d) { return n / d + (i64)(n % d != 0); } // 음수일 때 이상하게 작동할 수 있음. inline i64 ROUND(i64 n, i64 d) { return n / d + (i64)((n % d) * 2 >= d); } const i64 MOD = 1e9+7; inline i64 POW(i64 a, i64 n) { assert(0 <= n); i64 ret; for(ret = 1; n; a = a*a%MOD, n /= 2) { if(n%2) ret = ret*a%MOD; } return ret; } template <class T> ostream& operator<<(ostream& os, vector<T> v) { os << "["; int cnt = 0; for(auto vv : v) { os << vv; if(++cnt < v.size()) os << ","; } return os << "]"; } template <class T> ostream& operator<<(ostream& os, set<T> v) { os << "["; int cnt = 0; for(auto vv : v) { os << vv; if(++cnt < v.size()) os << ","; } return os << "]"; } template <class L, class R> ostream& operator<<(ostream& os, pair<L, R> p) { return os << "(" << p.fi << "," << p.se << ")"; } void debug_out() { cerr << endl; } template <typename Head, typename... Tail> void debug_out(Head H, Tail... T) { cerr << " " << H, debug_out(T...); } // ....................................................... // const int MAXN = 1e5+10; int n, ar[MAXN*2]; vi pos[MAXN]; i64 dp[MAXN][2]; void input() { cin >> n; FOR(i, 0, 2*n) cin >> ar[i], --ar[i], pos[ar[i]].pb(i); } int solve() { dp[0][0] = dp[0][1] = pos[0][0] + pos[0][1]; FOR(i, 1, n) { FOR(j, 0, 2) { dp[i][j] = 0x7fffffffffffffff; FOR(k, 0, 2) { dp[i][j] = min(dp[i][j], dp[i-1][k] + abs(pos[i-1][k] - pos[i][j]) + abs(pos[i-1][k^1] - pos[i][j^1])); } } } FOR(i, 0, n) debug(dp[i][0], dp[i][1]); cout << min(dp[n-1][0], dp[n-1][1]) << ENDL; return 0; } // ................. main .................. // void execute() { input(), solve(); } int main(void) { #ifdef LOCAL_BOOKNU freopen("input.txt", "r", stdin); // freopen("out.txt", "w", stdout); #endif cin.tie(0), ios_base::sync_with_stdio(false); execute(); return 0; } // ......................................... //후기
B번부터 DP스러운게 나와서 상당히 당황스러웠다.
뭔가 그리디한 방법이 있을 것 같다는 생각이 들었지만, 그걸 생각하는 것보다 DP식을 구현하는게 더 빠르다고 판단했다.
DP식을 짜다 보니 결국 전이 상태에서 그리디한 방법이 있다는 것을 알았지만, 이미 DP를 짜버려서 그냥 제출했다.
C번
C번 문제:
그래프BruteForce$n \cdot m$크기의 갈 수 있는 곳과 갈 수 없는 곳으로 이루어진 맵이 주어진다.
임의의 두 갈 수 있는 곳을 터널을 뚫어 연결 할 수 있다고 할 때, 시작점에서 출발해 끝 점에 도착하기 위해 필요한 터널의 최소 cost를 구해야 한다.
단, 터널은 단 1번만 뚫을 수 있으며, 그냥 움직일 때는 상하좌우로 움직일 수 있고, cost가 필요하지 않다
두 지점 $(y_s, x_s)$, $(y_e, x_e)$를 잇는 터널을 뚫는 비용은 $(y_s-y_e)^2 + (x_s-x_e)^2$이다.
풀이 보기
맵의 크기가 크지 않기 때문에 단순하게 생각하면 편하다.
시작 점이 속한 컴포넌트와 끝 점이 속한 컴포넌트를 구한다.
만약 두 컴포넌트가 같다면 터널이 필요하지 않아서 답은 0이다.
서로 다른 컴포넌트라면 모든 정점 쌍에 대해 터널을 뚫어보는 방식으로 최소값을 구하면 된다.
소스코드 보기
#include <bits/stdc++.h> using namespace std; #ifdef LOCAL_BOOKNU #define debug(...) cerr << "[" << #__VA_ARGS__ << "]:", debug_out(__VA_ARGS__) #else #define debug(...) 42 #endif // ........................macro.......................... // #define FOR(i, f, n) for(int (i) = (f); (i) < (int)(n); ++(i)) #define RFOR(i, f, n) for(int (i) = (f); (i) >= (int)(n); --(i)) #define pb push_back #define emb emplace_back #define fi first #define se second #define ENDL '\n' #define sz(A) (int)(A).size() #define ALL(A) A.begin(), A.end() #define UNIQUE(c) (c).resize(unique(ALL(c)) - (c).begin()) #define next next9876 #define prev prev1234 typedef pair<int, int> ii; typedef pair<int, ii> iii; typedef vector<int> vi; typedef vector<vi> vvi; typedef vector<ii> vii; typedef vector<vii> vvii; typedef long long i64; typedef unsigned long long ui64; // inline i64 GCD(i64 a, i64 b) { if(b == 0) return a; return GCD(b, a % b); } inline int getidx(const vi& ar, int x) { return lower_bound(ALL(ar), x) - ar.begin(); } // 좌표 압축에 사용: 정렬된 ar에서 x의 idx를 찾음 inline i64 GCD(i64 a, i64 b) { i64 n; if(a < b) swap(a, b); while(b != 0) { n = a % b; a = b; b = n; } return a; } inline i64 LCM(i64 a, i64 b) { if(a == 0 || b == 0) return GCD(a, b); return a / GCD(a, b) * b; } inline i64 CEIL(i64 n, i64 d) { return n / d + (i64)(n % d != 0); } // 음수일 때 이상하게 작동할 수 있음. inline i64 ROUND(i64 n, i64 d) { return n / d + (i64)((n % d) * 2 >= d); } const i64 MOD = 1e9+7; inline i64 POW(i64 a, i64 n) { assert(0 <= n); i64 ret; for(ret = 1; n; a = a*a%MOD, n /= 2) { if(n%2) ret = ret*a%MOD; } return ret; } template <class T> ostream& operator<<(ostream& os, vector<T> v) { os << "["; int cnt = 0; for(auto vv : v) { os << vv; if(++cnt < v.size()) os << ","; } return os << "]"; } template <class T> ostream& operator<<(ostream& os, set<T> v) { os << "["; int cnt = 0; for(auto vv : v) { os << vv; if(++cnt < v.size()) os << ","; } return os << "]"; } template <class L, class R> ostream& operator<<(ostream& os, pair<L, R> p) { return os << "(" << p.fi << "," << p.se << ")"; } void debug_out() { cerr << endl; } template <typename Head, typename... Tail> void debug_out(Head H, Tail... T) { cerr << " " << H, debug_out(T...); } // ....................................................... // const int MAXN = 50; const int dy[4] = { 0, 0, -1, 1 }, dx[4] = { -1, 1, 0, 0 }; int n, vis[MAXN][MAXN]; ii str, fin; vii ar, br; string g[MAXN]; void input() { cin >> n >> str.first >> str.second >> fin.first >> fin.second; FOR(i, 0, n) cin >> g[i]; } void f(int y, int x, vii& lis) { lis.pb({ y, x }); vis[y][x] = 1; FOR(dir, 0, 4) { int ny = y + dy[dir], nx = x + dx[dir]; if(0 <= ny && ny < n && 0 <= nx && nx < n && g[ny][nx] == '0' && !vis[ny][nx]) { f(ny, nx, lis); } } } i64 dis(ii& s, ii& e) { i64 a = s.first, b = s.second, c = e.first, d = e.second; return (a-c)*(a-c) + (b-d)*(b-d); } int solve() { --str.first, --str.second, --fin.first, --fin.second; f(str.first, str.second, ar); if(vis[fin.first][fin.second]) { cout << 0 << ENDL; return 0; } i64 ans = 0x7fffffffffffffff; f(fin.first, fin.se, br); FOR(i, 0, ar.size()) { FOR(j, 0, br.size()) { ans = min(ans, dis(ar[i], br[j])); } } cout << ans << ENDL; return 0; } // ................. main .................. // void execute() { input(), solve(); } int main(void) { #ifdef LOCAL_BOOKNU freopen("input.txt", "r", stdin); // freopen("out.txt", "w", stdout); #endif cin.tie(0), ios_base::sync_with_stdio(false); execute(); return 0; } // ......................................... //D1번
D1번 문제:
BruteForce그리디$n$개의 기차역이 원형으로 이어져있다. (즉, $1 \rightarrow 2 \rightarrow … \rightarrow n \rightarrow 1$)
$m$개의 화물을 운반해야 하는데, 각 화물은 시작역과 끝 역으로 이루어져 있으며, 시작역에서 화물을 싣고 끝 역에서 화물을 내려야 한다.
이 때, 기차의 적재량은 무한대이지만, 한 역에서는 1개의 화물 밖에 싣지 못한다.
$n$개의 역 각각에서 기차가 출발했을 때 모든 화물을 나르기 위한 최소 시간을 구해야 한다.
풀이 보기
이 문제는 $n$과 $m$값이 작기 때문에 단순하게 생각해보자.
일단 화물을 내리는 것은 기차에 있는걸 해당 역이 되면 그냥 내려버리면 되기 때문에 신경 쓸 필요가 없는데, 현재 역에 여러 화물이 있을 때 그 중 어떤 화물을 먼저 실을지가 문제다.
직관적으로 생각하면 먼 거리를 가는 화물을 우선적으로 싣는 것이 무조건 이득이라는 것을 알 수 있다.
짧은 거리를 가는 화물을 먼저 실어버리면 어차피 먼 거리를 가는 화물을 실으러 다시 이 역에 와야 하고, 그렇게 되면 먼 거리를 가는 화물이 남는 것이 손해이기 때문이다.
따라서 각 역마다 존재하는 화물들을 거리 역순으로 정렬해두고 시뮬레이팅 하면 된다.
소스코드 보기
#include <bits/stdc++.h> using namespace std; #ifdef LOCAL_BOOKNU #define debug(...) cerr << "[" << #__VA_ARGS__ << "]:", debug_out(__VA_ARGS__) #else #define debug(...) 42 #endif // ........................macro.......................... // #define FOR(i, f, n) for(int (i) = (f); (i) < (int)(n); ++(i)) #define RFOR(i, f, n) for(int (i) = (f); (i) >= (int)(n); --(i)) #define pb push_back #define emb emplace_back #define fi first #define se second #define ENDL '\n' #define sz(A) (int)(A).size() #define ALL(A) A.begin(), A.end() #define UNIQUE(c) (c).resize(unique(ALL(c)) - (c).begin()) #define next next9876 #define prev prev1234 typedef pair<int, int> ii; typedef pair<int, ii> iii; typedef vector<int> vi; typedef vector<vi> vvi; typedef vector<ii> vii; typedef vector<vii> vvii; typedef long long i64; typedef unsigned long long ui64; // inline i64 GCD(i64 a, i64 b) { if(b == 0) return a; return GCD(b, a % b); } inline int getidx(const vi& ar, int x) { return lower_bound(ALL(ar), x) - ar.begin(); } // 좌표 압축에 사용: 정렬된 ar에서 x의 idx를 찾음 inline i64 GCD(i64 a, i64 b) { i64 n; if(a < b) swap(a, b); while(b != 0) { n = a % b; a = b; b = n; } return a; } inline i64 LCM(i64 a, i64 b) { if(a == 0 || b == 0) return GCD(a, b); return a / GCD(a, b) * b; } inline i64 CEIL(i64 n, i64 d) { return n / d + (i64)(n % d != 0); } // 음수일 때 이상하게 작동할 수 있음. inline i64 ROUND(i64 n, i64 d) { return n / d + (i64)((n % d) * 2 >= d); } const i64 MOD = 1e9+7; inline i64 POW(i64 a, i64 n) { assert(0 <= n); i64 ret; for(ret = 1; n; a = a*a%MOD, n /= 2) { if(n%2) ret = ret*a%MOD; } return ret; } template <class T> ostream& operator<<(ostream& os, vector<T> v) { os << "["; int cnt = 0; for(auto vv : v) { os << vv; if(++cnt < v.size()) os << ","; } return os << "]"; } template <class T> ostream& operator<<(ostream& os, set<T> v) { os << "["; int cnt = 0; for(auto vv : v) { os << vv; if(++cnt < v.size()) os << ","; } return os << "]"; } template <class L, class R> ostream& operator<<(ostream& os, pair<L, R> p) { return os << "(" << p.fi << "," << p.se << ")"; } void debug_out() { cerr << endl; } template <typename Head, typename... Tail> void debug_out(Head H, Tail... T) { cerr << " " << H, debug_out(T...); } // ....................................................... // const int MAXN = 101, MAXM = 201; int n, m, cur[MAXN]; vi to[MAXN]; void input() { cin >> n >> m; FOR(i, 0, m) { int u, v; cin >> u >> v; --u, --v; to[u].pb((v+n - u) % n); } } int solve() { FOR(i, 0, n) sort(ALL(to[i]), greater<int>()), debug(to[i]); FOR(s, 0, n) { memset(cur, 0, sizeof(cur)); i64 ans = 0; int p = s, cnt = 0, rem = 0; while(cnt != m || rem > 0) { //FOR(i, 0, n) cout << cur[i] << ' '; cout << ENDL; --rem; if(cur[p] < to[p].size()) rem = max(rem, to[p][cur[p]]), ++cnt, ++cur[p]; // 현재에서 태울 수 있는거 태움 ++ans; p = (p+1)%n; } cout << ans -1 << ' '; } cout << ENDL; return 0; } // ................. main .................. // void execute() { input(), solve(); } int main(void) { #ifdef LOCAL_BOOKNU freopen("input.txt", "r", stdin); // freopen("out.txt", "w", stdout); #endif cin.tie(0), ios_base::sync_with_stdio(false); execute(); return 0; } // ......................................... //D2번
D2번 문제:
그리디D1번 문제에서 $n$, $m$이 증가했다.
풀이 보기
D1의 풀이에서 조금 더 관찰할 수 있는 것이 있다.
왜 하나의 역에서 먼 거리의 화물을 우선적으로 실을까?
바로 화물이 남아 있는 한, 해당 역으로 다시 되돌아와야 하기 때문이다.
이왕 되돌아와야 할 거, 먼 거 먼저 보내버리자는 심보이다.
그렇다면 어차피 다시 역으로 돌아와야 하는데, 이걸 시뮬레이팅 하는 것은 바보짓이 아닌가?
화물이 남아 있는 한 $n$초를 추가하면 될 것을 시뮬레이팅 하는 것은 계산 낭비이다.
이것을 일반화하면 다음과 같다.
각 역에서 열차가 출발 할 때 해당 역의 화물을 모두 배송하는 최소 시간은 $n \cdot (num-1) + shortest$ 이다.
이 때, $num$ = 해당 역의 화물 수, $shortest$ = 해당 역에서 가장 가까운 배송거리
그렇다면 해당 역에서 열차가 출발하지 않는 경우는 어떨까?
출발역에서 해당역까지의 거리를 더해주면 끝이라는 것을 쉽게 알 수 있다.
완전히 식을 일반화 해서 $s$역에서 출발할 때의 최소값을 구하려면 다음을 구하면 된다.
$max(dist(s, i) + n \cdot (num[i]-1) + shortest[i])\ \ \ for\ i = [1..n]$
소스코드 보기
#include <bits/stdc++.h> using namespace std; #ifdef LOCAL_BOOKNU #define debug(...) cerr << "[" << #__VA_ARGS__ << "]:", debug_out(__VA_ARGS__) #else #define debug(...) 42 #endif // ........................macro.......................... // #define FOR(i, f, n) for(int (i) = (f); (i) < (int)(n); ++(i)) #define RFOR(i, f, n) for(int (i) = (f); (i) >= (int)(n); --(i)) #define pb push_back #define emb emplace_back #define fi first #define se second #define ENDL '\n' #define sz(A) (int)(A).size() #define ALL(A) A.begin(), A.end() #define UNIQUE(c) (c).resize(unique(ALL(c)) - (c).begin()) #define next next9876 #define prev prev1234 typedef pair<int, int> ii; typedef pair<int, ii> iii; typedef vector<int> vi; typedef vector<vi> vvi; typedef vector<ii> vii; typedef vector<vii> vvii; typedef long long i64; typedef unsigned long long ui64; // inline i64 GCD(i64 a, i64 b) { if(b == 0) return a; return GCD(b, a % b); } inline int getidx(const vi& ar, int x) { return lower_bound(ALL(ar), x) - ar.begin(); } // 좌표 압축에 사용: 정렬된 ar에서 x의 idx를 찾음 inline i64 GCD(i64 a, i64 b) { i64 n; if(a < b) swap(a, b); while(b != 0) { n = a % b; a = b; b = n; } return a; } inline i64 LCM(i64 a, i64 b) { if(a == 0 || b == 0) return GCD(a, b); return a / GCD(a, b) * b; } inline i64 CEIL(i64 n, i64 d) { return n / d + (i64)(n % d != 0); } // 음수일 때 이상하게 작동할 수 있음. inline i64 ROUND(i64 n, i64 d) { return n / d + (i64)((n % d) * 2 >= d); } const i64 MOD = 1e9+7; inline i64 POW(i64 a, i64 n) { assert(0 <= n); i64 ret; for(ret = 1; n; a = a*a%MOD, n /= 2) { if(n%2) ret = ret*a%MOD; } return ret; } template <class T> ostream& operator<<(ostream& os, vector<T> v) { os << "["; int cnt = 0; for(auto vv : v) { os << vv; if(++cnt < v.size()) os << ","; } return os << "]"; } template <class T> ostream& operator<<(ostream& os, set<T> v) { os << "["; int cnt = 0; for(auto vv : v) { os << vv; if(++cnt < v.size()) os << ","; } return os << "]"; } template <class L, class R> ostream& operator<<(ostream& os, pair<L, R> p) { return os << "(" << p.fi << "," << p.se << ")"; } void debug_out() { cerr << endl; } template <typename Head, typename... Tail> void debug_out(Head H, Tail... T) { cerr << " " << H, debug_out(T...); } // ....................................................... // const int MAXN = 5001, MAXM = 20001; i64 n, m, cc[MAXN], to[MAXN]; // cc: i의 총 캔디 수 void input() { cin >> n >> m; FOR(i, 0, m) { int u, v; cin >> u >> v; --u, --v; if(to[u] == 0) to[u] = (v+n - u) % n; else to[u] = min(to[u], (v+n - u) % n); ++cc[u]; } } int solve() { //FOR(i, 0, n) debug(cc[i], to[i]); FOR(s, 0, n) { i64 ans = 0; FOR(i, 0, n) { if(cc[i]) { //debug(s, i, (i+n-s)%n, (cc[i]-1)*n + to[i]); ans = max(ans, (i64)(i+n-s)%n + (cc[i]-1)*n + to[i]);; } } cout << ans << ' '; } cout << ENDL; return 0; } // ................. main .................. // void execute() { input(), solve(); } int main(void) { #ifdef LOCAL_BOOKNU freopen("input.txt", "r", stdin); // freopen("out.txt", "w", stdout); #endif cin.tie(0), ios_base::sync_with_stdio(false); execute(); return 0; } // ......................................... //후기
실수로 D1번의 소스코드를 사용하다가 $n$, $m$범위를 바꾸지 않아 1번의 WA를 받았다.
이렇게 범위만 다른 류의 문제를 풀면 꼭 이런 실수를 하게 되는데, 조심해야겠다.
E번
E번 문제:
그리디ConstructiveAlgorithmsMath$n$개의 원소를 가진 배열 중, 연속한 원소들에 대해 $\max\limits_{0 \leq l \leq r \leq n-1} \sum\limits_{l \leq i \leq r} (r-l+1) \cdot a_i$ 를 찾는 문제가 있다.
(단, $1 \leq n \leq 2,000$ 이고 $abs(a_i) \leq 10^6$)
이 문제를 아래와 같은 코드로 구현했는데, 사실 이 코드는 예외가 존재하는 코드이다.
function find_answer(n, a) # Assumes n is an integer between 1 and 2000, inclusive # Assumes a is a list containing n integers: a[0], a[1], ..., a[n-1] res = 0 cur = 0 k = -1 for i = 0 to i = n-1 cur = cur + a[i] if cur < 0 cur = 0 k = i res = max(res, (i-k)*cur) return res$1 \leq k \leq 10^9$인 $k$가 주어질 때, 원래의 답과 이 코드의 답의 차이가 $k$가 되도록 하는 테스트케이스를 만들어야 한다.
(단, 테스트 케이스는 위에 명시된 $n$, $a_i$의 기준을 만족해야 한다.)
풀이 보기
우선 소스코드를 분석해보자.
이 코드는 $i = [0..n)$을 순회하며, sum의 시작 구간 $j$를 유지하며 만약 $\sum\limits_{j \leq idx \leq i} a_{idx}$가 음수가 된다면 시작 구간을 $i$로 옮겨버리고, 각 $i$마다 위의 식대로 값을 구한 뒤 그 중 최대값을 취하는 방법을 사용한다.
이 방법은 여러가지 문제점이 있지만, 나는 위의 코드가 선택한 구간 앞의 음수를 포함한 경우가 결과 값이 더 클 수 있다는 것에 주목했다.
즉, $\lbrace -1, 100 \rbrace$이 있을 때 위의 코드는 $100$을 반환하는데, 사실은 답이 $99 \cdot 2 = 198$이라는 것이다.
이것을 이용하면 위의 코드와 정답의 차이를 정확히 $k$로 만들 수 있을 것 같다.
우선 위와 같이 $\lbrace -1, a \rbrace$ 처럼 배열을 구성한다고 생각하면,
코드: $a$
정답: $2 \cdot (a-1)$
$\therefore k = 2 \cdot (a-1) - a = a - 2$
위와 같이 깔끔하게 해당되는 $a$값을 구할 수 있다.
하지만 한 가지 문제점은, $abs(a_i) \leq 10^6$를 만족시키는 배열을 만들어야 한다는 것이다.
따라서 $a$가 너무 커질 경우, 앞에 있는 $-1$을 점점 늘려가는 식으로 생각해보자.
즉, $\lbrace …, -1, -1, a \rbrace$처럼 배열을 구성하는 것이다.
또한 굳이 앞을 $-1$만 쓸 것이 아니라, $0$을 써도 상관 없다는 것을 유념하자.
이것을 통해 식을 세우면
$a$ 앞의 숫자의 개수 = $y$, -($a$ 앞의 숫자의 합) = $x$
코드: $a$
정답: $(y+1) \cdot (a-x) = a \cdot y - x \cdot y + a - x$
$k = (y+1) \cdot (a-x) = a \cdot y - x \cdot y + a - x - a = a \cdot y - x \cdot y - x$
$\therefore a = \frac{k + x}{y} + x$
이 때, $0 \leq x \leq y$를 만족하면서 $(k + x) \equiv 0 \pmod y$이 되는 $x$를 찾으면 되는데, 그것에 해당되는 것이 $x = y - (k \bmod y)$ 이다.
이제 $y = [1..2000)$을 순회하며 $a$가 조건 범위 내로 들어오는 경우에 대해서 출력해주면 된다.
이 방법이 반드시 답을 찾을 수 있는 이유는, 우선 $k$가 어떤 수이든 해당되는 $x$는 반드시 존재하게 된다.
또한 $y$가 점점 늘어감에 따라 단계별로 답과 코드의 차이가 $O(a)$만큼 벌어지게 되므로, $a$는 최대 $10^6$이고 $y$는 최대 $1,999$이므로 $10^9$이하인 $k$에 대해서 항상 조건에 맞는 $a$를 찾을 수 있다.
소스코드 보기
#include <bits/stdc++.h> using namespace std; #ifdef LOCAL_BOOKNU #define debug(...) cerr << "[" << #__VA_ARGS__ << "]:", debug_out(__VA_ARGS__) #else #define debug(...) 42 #endif // ........................macro.......................... // #define FOR(i, f, n) for(int (i) = (f); (i) < (int)(n); ++(i)) #define RFOR(i, f, n) for(int (i) = (f); (i) >= (int)(n); --(i)) #define pb push_back #define emb emplace_back #define fi first #define se second #define ENDL '\n' #define sz(A) (int)(A).size() #define ALL(A) A.begin(), A.end() #define UNIQUE(c) (c).resize(unique(ALL(c)) - (c).begin()) #define next next9876 #define prev prev1234 typedef pair<int, int> ii; typedef pair<int, ii> iii; typedef vector<int> vi; typedef vector<vi> vvi; typedef vector<ii> vii; typedef vector<vii> vvii; typedef long long i64; typedef unsigned long long ui64; // inline i64 GCD(i64 a, i64 b) { if(b == 0) return a; return GCD(b, a % b); } inline int getidx(const vi& ar, int x) { return lower_bound(ALL(ar), x) - ar.begin(); } // 좌표 압축에 사용: 정렬된 ar에서 x의 idx를 찾음 inline i64 GCD(i64 a, i64 b) { i64 n; if(a < b) swap(a, b); while(b != 0) { n = a % b; a = b; b = n; } return a; } inline i64 LCM(i64 a, i64 b) { if(a == 0 || b == 0) return GCD(a, b); return a / GCD(a, b) * b; } inline i64 CEIL(i64 n, i64 d) { return n / d + (i64)(n % d != 0); } // 음수일 때 이상하게 작동할 수 있음. inline i64 ROUND(i64 n, i64 d) { return n / d + (i64)((n % d) * 2 >= d); } const i64 MOD = 1e9+7; inline i64 POW(i64 a, i64 n) { assert(0 <= n); i64 ret; for(ret = 1; n; a = a*a%MOD, n /= 2) { if(n%2) ret = ret*a%MOD; } return ret; } template <class T> ostream& operator<<(ostream& os, vector<T> v) { os << "["; int cnt = 0; for(auto vv : v) { os << vv; if(++cnt < v.size()) os << ","; } return os << "]"; } template <class T> ostream& operator<<(ostream& os, set<T> v) { os << "["; int cnt = 0; for(auto vv : v) { os << vv; if(++cnt < v.size()) os << ","; } return os << "]"; } template <class L, class R> ostream& operator<<(ostream& os, pair<L, R> p) { return os << "(" << p.fi << "," << p.se << ")"; } void debug_out() { cerr << endl; } template <typename Head, typename... Tail> void debug_out(Head H, Tail... T) { cerr << " " << H, debug_out(T...); } // ....................................................... // const i64 RANGE = 1e6+1; i64 k; void input() { cin >> k; } int solve() { for(i64 y = 1; y < 2000; ++y) { i64 x = y - (k % y); i64 res = (k + x*y + x) / y; debug(y, x, res); if(res < RANGE) { cout << y+1 << ENDL; i64 ans = res; int p = 0; while(x < y-p) cout << 0 << ' ', p++; for(; p < y; ++p) { cout << -1 << ' '; } cout << ans << ENDL; return 0; } } assert(false); cout << -1 << ENDL; return 0; } // ................. main .................. // void execute() { input(), solve(); } int main(void) { #ifdef LOCAL_BOOKNU freopen("input.txt", "r", stdin); // freopen("out.txt", "w", stdout); #endif cin.tie(0), ios_base::sync_with_stdio(false); execute(); return 0; } // ......................................... //후기
처음에는 위와 같은 방식으로 접근했다가, 항상 맨 앞부분에 $-1$만을 넣어야 한다고 생각했었다.
(즉, $x = y$라고 생각함.)
따라서 $k \neq 0 \pmod y$인 경우에는 다음 $y$로 넘어가버리게 되서 $k$의 모든 소인수가 $2,000$이 넘어가버리는 경우 답이 존재함에도 불구하고 모든 $y$루프를 돌고 $-1$을 출력해버렸다.
하지만 생각해보니 $-1$뿐 아니라 $0$도 출력할 수 있다는 것을 깨닫고, 이것을 활용하면 $k$의 소인수가 어떻게 됐든 무조건 $y$로 나누어 떨어지게 할 수 있는 방법이 있다는 것을 깨달았다.
이 문제까지 푼 덕분에 꽤 많은 점수가 오를 수 있었다.
후기
컨테스트 시작은 별로 좋지 못했다.
A번에서 문제를 이해하는데 너무 오래걸렸고, 그나마도 조건을 잘못 읽어 2번이나 삽질해버렸다.
B번도 잘 생각했다면 그리디로 빠르게 풀고 넘어갈 수 있었는데, DP로 접근하는 바람에 “B번 문제인데 정말로 DP로 푸는거 맞나?”라는 생각과 DP 검증 때문에 솔브가 늦어졌다.
C번 역시 문제를 제대로 읽지 않고 일반 이동에는 코스트가 없다는 것을 읽지 못해 이상한 코드를 짜다가 늦어버렸다.
D번 부터는 꽤나 잘 풀린 편인데, 우선 D1은 시뮬레이팅 하면서 빠르고 확실하게 풀자고 생각했고, D2같은 경우는 실수로 수의 범위를 바꾸지 않고 제출해서 1번 틀린게 아까웠다.
E번 같은 경우는 처음 생각했던 방법이 방향성이 옳아서 쉽게 풀 수 있었던 것 같다.
다른 방법으로 접근했다면 푸는데 꽤 오래걸렸을텐데, 이걸 생각하면 운이 좋았던 것 같다.
아무튼 결과가 좋고 퍼플을 가게 되어서 상당히 기분 좋은 컨테스트였다.

-
백준 BOJ 15455 - [USACO Platinum] Push a Box
문제
BOJ 15455(https://www.acmicpc.net/problem/15455)
$n \cdot m$ 크기의 맵이 주어진다.
이 맵에는 걸어갈 수 있는 곳
.벽으로 막힌 곳#사람의 시작 위치A박스의 시작 위치B가 주어진다.그 후 $q$개의 쿼리가 주어지는데, $A$가 박스 $B$를 밀고 갈 때 해당 주어진 쿼리의 위치로 박스를 옮길 수 있는지를 출력해야 한다.
이 때, 박스를 민다는 것은, $A$가 박스의 바로 옆(혹은 위, 아래)에 붙어서 $A \rightarrow B$방향으로 박스를 민다는 것이다.
풀이
꽤나 복잡한 그래프 문제이다.
일단 박스가 스스로 움직이는게 아닌, 사람이 밀어줘야 한다는 제약조건이 크다.
차근차근 생각해보면, 일단 그래프의 탐색 공간은 박스가 각 셀에 위치할 경우 각각이 공간이 되니까 $O(n \cdot m)$이다.
그러나, 박스 뿐만 아니라 현재 사람의 위치도 고려해야 한다.
해당 셀에서 박스 주변 4방향 중 사람이 현재 어디있는지를 추가적으로 저장해야 하므로, 총 탐색공간은 $4 \cdot n \cdot m$일 것이다.
이제 초기 위치에서부터 갈 수 있는 모든 탐색 공간을
BFS로 탐사하면 되는데, 현재 공간에서 다음 공간으로 이동할 수 있는지 여부를 아는 것이 중요하다.현재 $(y, x)$에 박스가 있고 사람이 박스 주변의 $d$방향에 있을 때 박스에 인접한 다음 위치 $(ny, nx)$와 해당 위치로 밀고 가기 위한 사람의 방향 $nd$로 갈 수 있을까?
위에 대한 대답을 빠르게 들어야 하는데, 위의 문제를 정리해서 생각하면, 다음 두 가지를 만족해야 한다는 것을 알 수 있다.
- 애초에 $(ny, nx)$가 벽이 아닌가?
- 현재 사람의 위치 $(y, x)$의 $d$방향에서 다음 위치로 밀고 가기 위한 방향 $(y, x)$의 $nd$방향으로 사람이 움직일 수 있는가?
$1$번에 대한 답은 쉽게 구할 수 있는데, $2$번이 문제다.
$2$번을 조금 더 간략화하면 다음과 같다.
그래프에서 $(y, x)$를 거치지 않는 두 정점 사이의 path가 존재하는가?
일단 두 정점이 서로 다른 connected component에 존재할 경우 경로가 존재하지 않는다는 것은 자명하다.
문제는 두 정점이 하나의 connected component에 존재할 때 $(y, x)$를 지나지 않는 path가 존재하는지를 알아야 한다는 것인데, 이것을 위해서
DFS Spanning Tree에 대한 이해가 필요하다.무향그래프에서
DFS Spanning Tree를 만들었을 때 원래 그래프의 간선들은트리 간선혹은역 간선둘 중 하나로 분류 된다.방향 그래프에서
교차 간선과순 간선이 추가적으로 존재한다는 것에 비해 생각할 것이 훨씬 적어진다.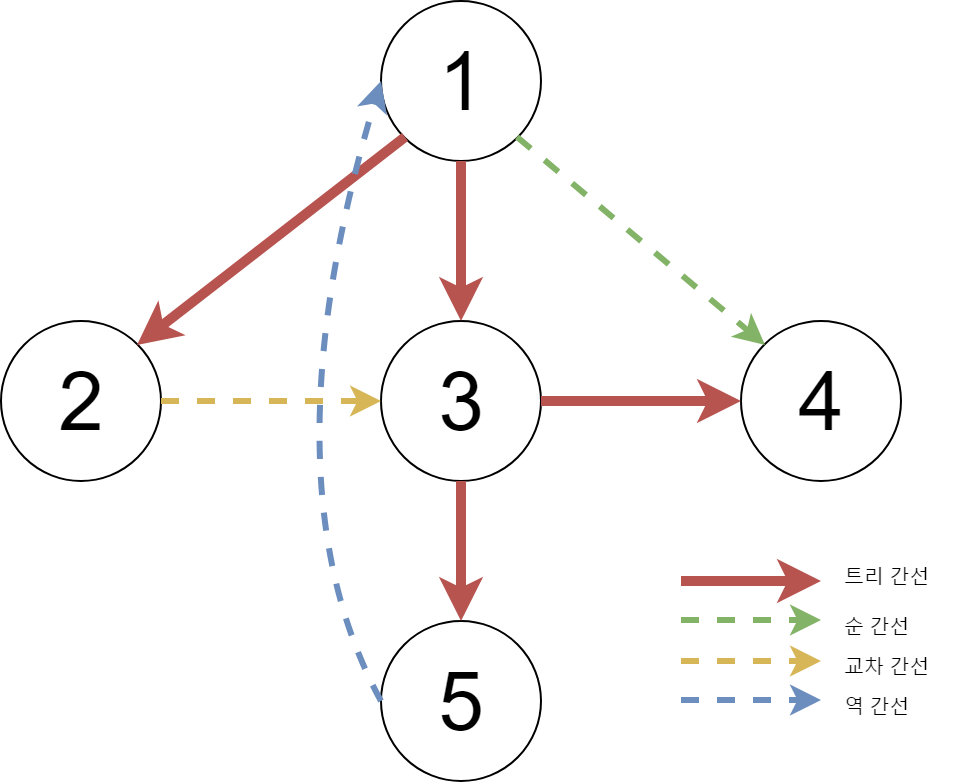
위 그림은 간선 분류에 대한 이해를 돕기 위한 그림인데, 방향 그래프이고 탐색 순서는 $1 \rightarrow 3 \rightarrow 5 \rightarrow 4 \rightarrow 2$ 이다.
만약 방향성이 없는 그래프라면
교차 간선과순 간선은 절대 존재하지 않는다.순 간선은 곧역 간선이라고 볼 수 있고,교차 간선같은 경우는 $u \rightarrow v$가 교차 간선이려면 $u$, $v$가 조상, 자손 관계가 아니면서 $v$의 dfs가 이미 끝난 상태에서 $u$의 dfs에서 $v$를 방문하면서 생기게 된다.그러나 무향그래프에서는 $v$의 dfs 상태에서 $u$를 방문하지 않았을 리 없고, 결과적으로
교차 간선이 생긴다는 것은 모순이다.아무튼 그래프에서 $x$를 지나지 않는 $path(u \rightarrow v)$가 존재하는지($cango(u, v, x)$) 확인하려면, 우선
DFS Spanning Tree를 생성해야 한다.그 후 트리의 각 정점마다 “$subtree(node)$에서 최대로 조상으로 올라갈 수 있는 역간선 = $up[node]$”을 절단점 구하기 알고리즘을 약간 변형한 방법으로 모두 구해놓는다.
이제 실제로 $cango(u, v, x)$를 계산해야 하는데, $t = lca(u, v)$를 구하고 만약 $x$가 $path(t, u)$ 혹은 $path(t, v)$ 사이에 존재하지 않는다면 무조건 가능한 경우이다.

만약 $t=x$라면, $path(t, u)$중 $t$의 자식인 정점을 $child(t, u)$라고 할 때, $up[child(t, u)]$와 $up[child(t, v)]$ 모두 $x$보다 조상 노드로 갈 수 있어야 한다.

만약 $t \ne x$라면, $up[child(t, u\ or\ v)]$가 $x$보다 조상 노드로 갈 수 있어야 한다.

$cango(u, v, x)$를 계산할 수 있게 되었으니 이것을 이용해 bfs를 통해
Flood Fill과 비슷하게 갈 수 있는 곳들을 체크해주고, 쿼리에서는 그 결과값만을 출력해주면 된다.소스코드
##include <bits/stdc++.h> using namespace std; #ifdef LOCAL_BOOKNU #define debug(...) cerr << "[" << #__VA_ARGS__ << "]:", debug_out(__VA_ARGS__) #else #define debug(...) 42 #endif // ........................macro.......................... // #define FOR(i, f, n) for(int (i) = (f); (i) < (int)(n); ++(i)) #define RFOR(i, f, n) for(int (i) = (f); (i) >= (int)(n); --(i)) #define pb push_back #define emb emplace_back #define fi first #define se second #define ENDL '\n' #define sz(A) (int)(A).size() #define ALL(A) A.begin(), A.end() #define UNIQUE(c) (c).resize(unique(ALL(c)) - (c).begin()) #define next next9876 #define prev prev1234 typedef pair<int, int> ii; typedef pair<int, ii> iii; typedef vector<int> vi; typedef vector<vi> vvi; typedef vector<ii> vii; typedef vector<vii> vvii; typedef long long i64; typedef unsigned long long ui64; // inline i64 GCD(i64 a, i64 b) { if(b == 0) return a; return GCD(b, a % b); } inline int getidx(const vi& ar, int x) { return lower_bound(ALL(ar), x) - ar.begin(); } // 좌표 압축에 사용: 정렬된 ar에서 x의 idx를 찾음 inline i64 GCD(i64 a, i64 b) { i64 n; if(a < b) swap(a, b); while(b != 0) { n = a % b; a = b; b = n; } return a; } inline i64 LCM(i64 a, i64 b) { if(a == 0 || b == 0) return GCD(a, b); return a / GCD(a, b) * b; } inline i64 CEIL(i64 n, i64 d) { return n / d + (i64)(n % d != 0); } // 음수일 때 이상하게 작동할 수 있음. inline i64 ROUND(i64 n, i64 d) { return n / d + (i64)((n % d) * 2 >= d); } inline i64 POW(i64 a, i64 n) { assert(0 <= n); i64 ret; for(ret = 1; n; a = a*a, n /= 2) { if(n%2) ret *= a; } return ret; } template <class T> ostream& operator<<(ostream& os, vector<T> v) { os << "["; int cnt = 0; for(auto vv : v) { os << vv; if(++cnt < v.size()) os << ","; } return os << "]"; } template <class T> ostream& operator<<(ostream& os, set<T> v) { os << "["; int cnt = 0; for(auto vv : v) { os << vv; if(++cnt < v.size()) os << ","; } return os << "]"; } template <class L, class R> ostream& operator<<(ostream& os, pair<L, R> p) { return os << "(" << p.fi << "," << p.se << ")"; } void debug_out() { cerr << endl; } template <typename Head, typename... Tail> void debug_out(Head H, Tail... T) { cerr << " " << H, debug_out(T...); } // ....................................................... // const int MAXN = 1501, MAXV = MAXN*MAXN, LOGN = 23; const int dy[4] = { 0, 0, -1, 1 }, dx[4] = { -1, 1, 0, 0 }; int n, m, nv, qq, did, ay, ax, by, bx, vis[MAXV], dep[MAXV], up[MAXV], par[MAXV][LOGN], chk[MAXV][4]; string mp[MAXN]; vi g[MAXV]; void input() { cin >> n >> m >> qq; FOR(i, 0, n) cin >> mp[i]; } int uidx(int y, int x) { return y*m+x; } bool valid(int y, int x) { return 0 <= y && y < n && 0 <= x && x < m; } // y, x를 root로 하는 하나의 컴포넌트로 이어진 그래프의 dfs 스패닝 트리를 만든다. void getComponent(int y, int x) { FOR(dir, 0, 4) { int ny = y + dy[dir], nx = x + dx[dir]; if(valid(ny, nx) && mp[ny][nx] != '#') { g[uidx(y, x)].pb(uidx(ny, nx)); if(par[uidx(ny, nx)][0] == -1) { par[uidx(ny, nx)][0] = uidx(y, x); getComponent(ny, nx); } } } } // dfs 스패닝 트리에서 각 node마다 vis 부여하고 최대로 갈 수 있는 역간선을 구한다. int dfs(int u) { int ret = vis[u] = did++; for(auto v : g[u]) { if(par[v][0] == u) { dep[v] = dep[u] + 1; ret = min(ret, dfs(v)); } else ret = min(ret, vis[v]); } return up[u] = ret; } // dfs 스패닝 트리에서 u, v의 lca int lca(int u, int v) { if(dep[u] < dep[v]) swap(u, v); int dif = dep[u] - dep[v]; FOR(i, 0, LOGN) if(dif & (1<<i)) u = par[u][i]; if(u != v) { RFOR(i, LOGN-1, 0) { if(par[u][i] != par[v][i]) { u = par[u][i], v = par[v][i]; } } u = par[u][0]; } return u; } // u가 v의 자식일 때 path(u->v) 중 v의 자식을 반환 int getchild(int u, int v) { int dif = dep[u] - dep[v]; for(int i = 1; dif != 1; ++i) { if(dif&(1<<i)) dif -= (1<<i), u = par[u][i]; } return u; } // x정점을 지나지 않고 u->v를 갈 수 있는지? // x != u, v인 것만 넣기!! // 무향 그래프에서는 무조건 역간선만 존재 bool cango(int u, int v, int x) { if(par[u][0] == -1 || par[v][0] == -1) return false; // 시작 끝 둘 중 하나라도 같은 컴포넌트가 아니면 불가 if(par[x][0] == -1) return true; // 같은 컴포넌트인데 방해꾼이 없으면 가능 int t = lca(u, v); if(x == t) { // t 자체가 잘리면? xuchild, xvchild->par[x]가 존재하는지 확인 return up[getchild(u, x)] < vis[x] && up[getchild(v, x)] < vis[x]; } else if(vis[t] <= vis[x] && vis[x] <= vis[u]) { // t->u사이가 잘리면? xuchild->par[x]가 존재하는지 확인 return up[getchild(u, x)] < vis[x]; } else if(vis[t] <= vis[x] && vis[x] <= vis[v]) { // t->v사이가 잘리면? xvchild->par[x]가 존재하는지 확인 return up[getchild(v, x)] < vis[x]; } return true; } int solve() { nv = n*m; memset(par, -1, sizeof(par)); FOR(y, 0, n) { FOR(x, 0, m) { if(mp[y][x] == 'A') { par[uidx(y, x)][0] = uidx(y, x); ay = y, ax = x; getComponent(y, x); } if(mp[y][x] == 'B') by = y, bx = x; } } FOR(j, 1, LOGN) { FOR(i, 0, nv) { par[i][j] = par[par[i][j-1]][j-1]; } } dfs(uidx(ay, ax)); queue<ii> q; FOR(dir, 0, 4) { int ny = by - dy[dir], nx = bx - dx[dir]; // 상자를 그 방향으로 밀 수 있는 위치로 이동 if(valid(ny, nx) && cango(uidx(ay, ax), uidx(ny, nx), uidx(by, bx))) q.push({ uidx(by, bx), dir }), chk[uidx(by, bx)][dir] = 1; } while(q.size()) { int u = q.front().first, d = q.front().second; q.pop(); int y = u/m, x = u%m, cy = y - dy[d], cx = x - dx[d]; // 현재 박스 위치, 현재 미는 곳 위치 FOR(dir, 0, 4) { int py = y - dy[dir], px = x - dx[dir]; // 밀 수 있는 곳으로 가야 함. if(dir == d || (valid(py, px) && cango(uidx(cy, cx), uidx(py, px), uidx(y, x)))) { // 해당 방향으로 밀 수 있으면 int ny = y + dy[dir], nx = x + dx[dir]; if(valid(ny, nx) && mp[ny][nx] != '#' && !chk[uidx(ny, nx)][dir]) { chk[uidx(ny, nx)][dir] = 1; q.push({ uidx(ny, nx), dir }); } } } } while(qq--) { int y, x; cin >> y >> x; --y, --x; if(y == by && x == bx) { cout << "YES" << ENDL; continue; } bool ans = false; FOR(dir, 0, 4) { if(chk[uidx(y, x)][dir]) { ans = 1; break; } } if(ans) cout << "YES" << ENDL; else cout << "NO" << ENDL; } return 0; } // ................. main .................. // void execute() { input(), solve(); } int main(void) { #ifdef LOCAL_BOOKNU freopen("input.txt", "r", stdin); // freopen("out.txt", "w", stdout); #endif cin.tie(0), ios_base::sync_with_stdio(false); execute(); return 0; } // ......................................... //
-
코드포스 Educational Codeforces Round #56(Div.2)(Virtual) 리뷰
개요
꽤 오래 전에 했던 버추얼있데, 시간이 좀 지나서 어떤 문제였는지 까먹었다.
E번을 구현하고 리뷰하려고 했지만, E 구현에 g++이 필요해 그 환경설정을 한다고 미뤄뒀다가 지금에서야 리뷰를 하게 됐다.
D번까지는 전반적으로 쉬웠고, E번에서 문제도 잘 단순화 했고, 적절한 자료구조를 사용했지만 비효율적인 구현으로 인해 TLE가 났다는 것이 아쉬웠다.
이 TLE가 발생하지 않고 조금 더 효율적으로 구현하려면 종만북에서 소개되는
Treap이라는 자료구조가 필요한데, 직접 구현하기에는 까다롭고g++에서 지원하는 order statistics tree를 사용하면 편하게 구현할 수 있다.에디토리얼에서는 이것 없이
Fenwick Tree와lower_bound를 적절히 사용해서 구현했는데, 이것도 리뷰 할 것이다.C번
C번 문제:
그리디구현$n$은 항상 짝수이며, $\frac{n}{2}$개의 음이 아닌 정수로 이루어진 $b_i$가 주어진다.
이 때, $b_i = a_i + a_{n-i+1}$을 만족시키고, 단조증가($a_i \leq a_{i+1}$)하며, 음이 아닌 정수로 이루어진 수열 $a_i$를 구해야 한다.
풀이 보기
$b_1$부터 차례로 만들어가면 되는데, 조건을 만족하는 한도에서 $a_i$는 현재 만들 수 있는 것 중에서 가장 작게, $a_{n-i+1}$은 가장 크게 만들어나가면 된다.
(이 때 둘 사이의 갭이 크면 클 수록 좋다.)
즉, $a_i \geq a_{i-1}$이며 $a_{n-i+1} \leq a_{n-i+2}$를 만족하는 경우 중 갭이 가장 큰 경우를 골라나가면 된다.
소스코드 보기
#include <bits/stdc++.h> using namespace std; #ifdef LOCAL_BOOKNU #define debug(...) cerr << "[" << #__VA_ARGS__ << "]:", debug_out(__VA_ARGS__) #else #define debug(...) 42 #endif // ........................macro.......................... // #define FOR(i, f, n) for(int (i) = (f); (i) < (int)(n); ++(i)) #define RFOR(i, f, n) for(int (i) = (f); (i) >= (int)(n); --(i)) #define pb push_back #define emb emplace_back #define fi first #define se second #define ENDL '\n' #define sz(A) (int)(A).size() #define ALL(A) A.begin(), A.end() #define UNIQUE(c) (c).resize(unique(ALL(c)) - (c).begin()) #define next next9876 #define prev prev1234 typedef pair<int, int> ii; typedef pair<int, ii> iii; typedef vector<int> vi; typedef vector<vi> vvi; typedef vector<ii> vii; typedef vector<vii> vvii; typedef long long i64; typedef unsigned long long ui64; // inline i64 GCD(i64 a, i64 b) { if(b == 0) return a; return GCD(b, a % b); } inline int getidx(const vi& ar, int x) { return lower_bound(ALL(ar), x) - ar.begin(); } // 좌표 압축에 사용: 정렬된 ar에서 x의 idx를 찾음 inline i64 GCD(i64 a, i64 b) { i64 n; if(a < b) swap(a, b); while(b != 0) { n = a % b; a = b; b = n; } return a; } inline i64 LCM(i64 a, i64 b) { if(a == 0 || b == 0) return GCD(a, b); return a / GCD(a, b) * b; } inline i64 CEIL(i64 n, i64 d) { return n / d + (i64)(n % d != 0); } // 음수일 때 이상하게 작동할 수 있음. inline i64 ROUND(i64 n, i64 d) { return n / d + (i64)((n % d) * 2 >= d); } inline i64 POW(i64 a, i64 n) { assert(0 <= n); i64 ret; for(ret = 1; n; a = a*a, n /= 2) { if(n%2) ret *= a; } return ret; } template <class T> ostream& operator<<(ostream& os, vector<T> v) { os << "["; int cnt = 0; for(auto vv : v) { os << vv; if(++cnt < v.size()) os << ","; } return os << "]"; } template <class T> ostream& operator<<(ostream& os, set<T> v) { os << "["; int cnt = 0; for(auto vv : v) { os << vv; if(++cnt < v.size()) os << ","; } return os << "]"; } template <class L, class R> ostream& operator<<(ostream& os, pair<L, R> p) { return os << "(" << p.fi << "," << p.se << ")"; } void debug_out() { cerr << endl; } template <typename Head, typename... Tail> void debug_out(Head H, Tail... T) { cerr << " " << H, debug_out(T...); } // ....................................................... // const int MAXN = 2e5+10; i64 n, ar[MAXN], br[MAXN]; void input() { cin >> n; FOR(i, 0, n/2) cin >> br[i]; } int solve() { i64 cur = 0; ar[0] = 0ll, ar[n-1] = br[0]; FOR(i, 1, n/2) { ar[n-i-1] = min(br[i]-ar[i-1], ar[n-i]); ar[i] = br[i]-ar[n-i-1]; } FOR(i, 0, n) cout << ar[i] << ' '; cout << ENDL; return 0; } // ................. main .................. // void execute() { input(), solve(); } int main(void) { #ifdef LOCAL_BOOKNU freopen("input.txt", "r", stdin); // freopen("out.txt", "w", stdout); #endif cin.tie(0), ios_base::sync_with_stdio(false); execute(); return 0; } // ......................................... //D번
D번 문제:
그래프그리디$n$개의 정점과 $m$개의 간선으로 이루어진 무향 무가중 그래프가 주어진다.
이 그래프에서 각 정점마다 $1$, $2$, $3$ 중 하나의 가중치를 부여하여, 모든 간선에 대해 간선의 양 끝 점의 합이 홀수가 되도록 하는 방법의 수를 구해야 한다.
풀이 보기
일단 간선의 양 끝 정점의 합이 홀수가 되게 한다는 것은, 정점들을 짝수, 홀수인 그룹으로 나눴을 때 두 정점은 서로 다른 그룹에 속해야 한다는 것이다.
주어진 그래프가 연결 그래프라는 소리는 없었으나, 일단 하나의 연결 그래프에 대해서만 고려해보자.
(여러개의 컴포넌트가 있을 경우는 그냥 각 컴포넌트의 경우의 수를 모두 곱하면 된다.)
임의의 한 시작 정점 $u$에 아무 가중치나 부여해보면 $u$와 연결된 정점 $v$들은 모두 $u$와 다른 가중치를 가져야 할 것이며, 이것은 BFS처럼 퍼져나가게 된다는 것을 알 수 있다.
만약 가중치를 부여해야 할 정점이 이미 가중치를 가지고 있고, 그것이 현재 정점과 같은 가중치이면 어떻게 하든 정점을 칠할 방법이 없는 것이다.
이와 같은 방법의 모든 정점에 색을 다 입힌 후에 시작 정점을 홀수로 칠하는 경우, 짝수로 칠하는 경우 각각에 대해서 경우의 수를 구해주면 된다.
(이 때, 홀수의 경우 $1$, $3$ 두 가지 경우로 칠할 수 있다는 것을 염두에 두어야 한다.)
소스코드 보기
#include <bits/stdc++.h> using namespace std; #ifdef LOCAL_BOOKNU #define debug(...) cerr << "[" << #__VA_ARGS__ << "]:", debug_out(__VA_ARGS__) #else #define debug(...) 42 #endif // ........................macro.......................... // #define FOR(i, f, n) for(int (i) = (f); (i) < (int)(n); ++(i)) #define RFOR(i, f, n) for(int (i) = (f); (i) >= (int)(n); --(i)) #define pb push_back #define emb emplace_back #define fi first #define se second #define ENDL '\n' #define sz(A) (int)(A).size() #define ALL(A) A.begin(), A.end() #define UNIQUE(c) (c).resize(unique(ALL(c)) - (c).begin()) #define next next9876 #define prev prev1234 typedef pair<int, int> ii; typedef pair<int, ii> iii; typedef vector<int> vi; typedef vector<vi> vvi; typedef vector<ii> vii; typedef vector<vii> vvii; typedef long long i64; typedef unsigned long long ui64; // inline i64 GCD(i64 a, i64 b) { if(b == 0) return a; return GCD(b, a % b); } inline int getidx(const vi& ar, int x) { return lower_bound(ALL(ar), x) - ar.begin(); } // 좌표 압축에 사용: 정렬된 ar에서 x의 idx를 찾음 inline i64 GCD(i64 a, i64 b) { i64 n; if(a < b) swap(a, b); while(b != 0) { n = a % b; a = b; b = n; } return a; } inline i64 LCM(i64 a, i64 b) { if(a == 0 || b == 0) return GCD(a, b); return a / GCD(a, b) * b; } inline i64 CEIL(i64 n, i64 d) { return n / d + (i64)(n % d != 0); } // 음수일 때 이상하게 작동할 수 있음. inline i64 ROUND(i64 n, i64 d) { return n / d + (i64)((n % d) * 2 >= d); } const i64 MOD = 998244353; inline i64 POW(i64 a, i64 n) { assert(0 <= n); i64 ret; for(ret = 1; n; a = (a*a) % MOD, n /= 2) { if(n%2) ret *= a, ret %= MOD; } return ret; } template <class T> ostream& operator<<(ostream& os, vector<T> v) { os << "["; int cnt = 0; for(auto vv : v) { os << vv; if(++cnt < v.size()) os << ","; } return os << "]"; } template <class T> ostream& operator<<(ostream& os, set<T> v) { os << "["; int cnt = 0; for(auto vv : v) { os << vv; if(++cnt < v.size()) os << ","; } return os << "]"; } template <class L, class R> ostream& operator<<(ostream& os, pair<L, R> p) { return os << "(" << p.fi << "," << p.se << ")"; } void debug_out() { cerr << endl; } template <typename Head, typename... Tail> void debug_out(Head H, Tail... T) { cerr << " " << H, debug_out(T...); } // ....................................................... // int n, m; vi ar; vvi g; set<int> rem; void input() { cin >> n >> m; g = vvi(n, vi()); ar = vi(n, -1); while(m--) { int u, v; cin >> u >> v; --u, --v; g[u].push_back(v); g[v].push_back(u); } } int solve() { i64 ans = 1; rem.clear(); FOR(i, 0, n) rem.insert(i); while(rem.size()) { vi cur; queue<int> q; q.push(*rem.begin()); ar[*rem.begin()] = 0; while(q.size()) { int u = q.front(); q.pop(); cur.pb(u); rem.erase(u); for(int v : g[u]) { if(ar[v] == -1) ar[v] = ar[u]^1, q.push(v); else if(ar[v] == ar[u]) { cout << 0 << ENDL; return 0; } } } int cnt = 0; for(int u : cur) { if(ar[u]) ++cnt; } ans *= ((POW(2, cnt) + POW(2, cur.size()-cnt)) % MOD); ans %= MOD; } cout << ans << ENDL; return 0; } // ................. main .................. // void execute() { int TT; cin >> TT; while(TT--) input(), solve(); } int main(void) { #ifdef LOCAL_BOOKNU freopen("input.txt", "r", stdin); // freopen("out.txt", "w", stdout); #endif cin.tie(0), ios_base::sync_with_stdio(false); execute(); return 0; } // ......................................... //E번
E번 문제:
쿼리SegTreeFenwickOrder Statistics Tree$n$개의 원소를 가진 두 수열 $a$, $b$가 있고, 각각은 $[1..n]$이 딱 $1$번씩만 등장한다.
이후 $q$개의 두 종류의 쿼리가 들어온다.
$1$ $s_a$ $e_a$ $s_b$ $e_b$ : $a[s_a..e_a]$와 $b[s_b..e_b]$에 공통으로 존재하는 원소의 수를 찾아라
$2$ $p$ $q$ : 수열 $b$에서 $p$, $q$의 위치를 바꿔라.
풀이 보기
한 쿼리를 $O(\log{n})$혹은 $O(\log^2{n})$만에 처리해야 한다.
$2$번 쿼리는 그냥 자리만 바꾸면 된다고 치고, $1$번 쿼리를 어떻게 처리해야 할까?
일단 기본적인 데이터를 가공하지 않고 $1$번을 처리하는 방법은 나로써는 $O(n)$ 밖에 생각이 나지 않는다.
이렇게 막막할 때마다 쓰기 좋았던 방법이 있는데, 바로 배열의 idx와 val의 위치를 바꾸는 것이다.
즉, $a[idx] = val$로 배열을 표현했다면, $a’[val] = idx$로 표현을 하는 것이다.
이런 방법은
Segment Tree문제들을 풀 때 종종 유용하게 사용된다.이로써 얻을 수 있는 이득은 서로 중복 여부를 확인하는데만 쓰였던 val을 index로 보내버렸다는 것에 있다.
사실 우리는 idx 구간에 존재하는 원소의 val을 알고 싶은게 아니다. val은 단지 중복 여부 판단에 쓰일 뿐이다.
여기서 중복 판단이란 두 idx가 같은 val을 가지고 있느냐는 것인데, 변형된 버전에서는 두 idx가 같은 index인가를 알아보는 것이다.
즉, $a[x] = b[y]$인지를 알고 싶다면, 변형된 배열$a’$, $b’$에서 각각 $x$, $y$가 등장하는 위치가 같은지를 알아보면 된다.
언뜻 보기에는 왜 이렇게 비효율적인 방법을 사용하는지 의문이 들 수 있지만, 이 방법은 두 배열의 “공유하는 index”를 이용한다는 장점이 있다.
두 배열이 공유하는 index를 가질 때만 같은 값을 가지는데, 이것을 아예 합쳐버리면 어떻게 될까?
즉, $ab[val] = (idx_a, idx_b)$ 형태로 만들어버리는 것이다.
이렇게 하면 값이 마치 2차원 평면에서의 좌표처럼 변하고, $1$번 쿼리를 다음과 같이 단순화 할 수 있다.
2차원 평면에 좌표들이 있을 때, 특정 $[(s_x, s_y), (e_x, e_y)]$구간에 속하는 점의 수를 구해라.
이 문제는 꽤나 전형적인 문제이고, 특히나 점의 수가 $2 \cdot 10^5$밖에 안 되는 상황에서는 효율적으로 쿼리를 처리할 수 있는 방법들이 있다.
첫 번째로는 쿼드트리를 사용하는 방법인데, 평면을 재귀적으로 4등분하여 탐색하는 방법이다.
점을 추가할 때는 $O(\log{n})$번의 재귀만을 거치면 되고, 구간 쿼리를 할 때 역시 $O(\log{n})$번의 재귀만을 거치면 된다.
단, 구간 쿼리 시 $O(\log{n})$에 붙는 상수 값이 크고, 점을 추가 할 때 현재 점을 가지고 있는 구간들을
map[구간]에 저장해두고 구간 쿼리 시 해당 구간이map에 존재하지 않는다면 탐색을 하지 않는 식으로 구현했는데, map 자체의 시간복잡도도 커서 TLE가 발생하였다.두 번째 방법은
2D segtree를 sparse하게 구현하는 것이다.sparse하지 않는
2D segtree의 경우 $x$축을 구간으로 나누고, 각 $x$축 구간마다 $y$를 저장하는segtree를 만드는 방식으로 구현된다.하지만 이렇게 구현을 하면 공간 복잡도가 $O(n^2)$이 돼 버리기 때문에 다른 방법을 생각해야 한다.
점의 수 자체가 적기 때문에, 각 $x$구간마다 $y$를
segtree로 저장하는 대신에set형태로 저장하면 공간을 효율적으로 사용 할 수 있다.점을 추가하는 쿼리는 그냥 $x$구간마다
set에insert를 하면 되지만, 구간 쿼리에서는set에서 $y$보다 작은 원소의 수를 빠르게 구해야한다.하지만 이 연산은
STL set에 구현되어 있지 않고,g++에 내장된 order statistics tree를 사용하면 쉽게 구현할 수 있다.세 번째 방법은 두 번째 방법에서 order statistics tree를 사용하지 않고 구현한 방법이다.
set을 두 개의 배열로 대신해서 구현을 한다.$vals$는 해당 $x$구간에 존재할 수 있는 $y$들을 저장하고, $f$는 그 $y$가 총 몇 개나 등장했는지를 저장한다.
이 때의 문제점이 $1$번 쿼리로 인해 해당 구간에 존재하는 $y$값이 바뀔 수 있다는 것인데, 이것은 모든 쿼리에 대해 전처리를 해서 해당 구간에 존재할 수 있는 모든 $y$를 저장해두면 해결된다.
쿼리의 수도 $O(2 \cdot 10^5$이기 때문에 시간복잡도에 대한 영향도 없다.
QuadTree를 사용한 코드 보기(TLE)
#include <bits/stdc++.h> using namespace std; #ifdef LOCAL_BOOKNU #define debug(...) cerr << "[" << #__VA_ARGS__ << "]:", debug_out(__VA_ARGS__) #else #define debug(...) 42 #endif // ........................macro.......................... // #define FOR(i, f, n) for(int (i) = (f); (i) < (int)(n); ++(i)) #define RFOR(i, f, n) for(int (i) = (f); (i) >= (int)(n); --(i)) #define pb push_back #define emb emplace_back #define fi first #define se second #define ENDL '\n' #define sz(A) (int)(A).size() #define ALL(A) A.begin(), A.end() #define UNIQUE(c) (c).resize(unique(ALL(c)) - (c).begin()) #define next next9876 #define prev prev1234 typedef pair<int, int> ii; typedef pair<int, ii> iii; typedef vector<int> vi; typedef vector<vi> vvi; typedef vector<ii> vii; typedef vector<vii> vvii; typedef long long i64; typedef unsigned long long ui64; // inline i64 GCD(i64 a, i64 b) { if(b == 0) return a; return GCD(b, a % b); } inline int getidx(const vi& ar, int x) { return lower_bound(ALL(ar), x) - ar.begin(); } // 좌표 압축에 사용: 정렬된 ar에서 x의 idx를 찾음 inline i64 GCD(i64 a, i64 b) { i64 n; if(a < b) swap(a, b); while(b != 0) { n = a % b; a = b; b = n; } return a; } inline i64 LCM(i64 a, i64 b) { if(a == 0 || b == 0) return GCD(a, b); return a / GCD(a, b) * b; } inline i64 CEIL(i64 n, i64 d) { return n / d + (i64)(n % d != 0); } // 음수일 때 이상하게 작동할 수 있음. inline i64 ROUND(i64 n, i64 d) { return n / d + (i64)((n % d) * 2 >= d); } inline i64 POW(i64 a, i64 n) { assert(0 <= n); i64 ret; for(ret = 1; n; a = a*a, n /= 2) { if(n%2) ret *= a; } return ret; } template <class T> ostream& operator<<(ostream& os, vector<T> v) { os << "["; int cnt = 0; for(auto vv : v) { os << vv; if(++cnt < v.size()) os << ","; } return os << "]"; } template <class T> ostream& operator<<(ostream& os, set<T> v) { os << "["; int cnt = 0; for(auto vv : v) { os << vv; if(++cnt < v.size()) os << ","; } return os << "]"; } template <class L, class R> ostream& operator<<(ostream& os, pair<L, R> p) { return os << "(" << p.fi << "," << p.se << ")"; } void debug_out() { cerr << endl; } template <typename Head, typename... Tail> void debug_out(Head H, Tail... T) { cerr << " " << H, debug_out(T...); } // ....................................................... // class FastIO { int fd, bufsz; char *buf, *cur, *end; public: FastIO(int _fd = 0, int _bufsz = 1 << 20) : fd(_fd), bufsz(_bufsz) { buf = cur = end = new char[bufsz]; } ~FastIO() { delete[] buf; } bool readbuf() { cur = buf; end = buf + bufsz; while(true) { size_t res = fread(cur, sizeof(char), end - cur, stdin); if(res == 0) break; cur += res; } end = cur; cur = buf; return buf != end; } int r() { while(true) { if(cur == end) readbuf(); if(isdigit(*cur) || *cur == '-') break; ++cur; } bool sign = true; if(*cur == '-') { sign = false; ++cur; } int ret = 0; while(true) { if(cur == end && !readbuf()) break; if(!isdigit(*cur)) break; ret = ret * 10 + (*cur - '0'); ++cur; } return sign ? ret : -ret; } } sc; const int MAXN = 1<<18; int n, qq, xr[MAXN], yr[MAXN], yidx[MAXN]; map<pair<ii, ii>, int> mp; void input() { n = sc.r(), qq = sc.r(); int p; FOR(i, 0, n) p = sc.r(), xr[p-1] = i; FOR(i, 0, n) p = sc.r(), yr[p-1] = i, yidx[i] = p-1; //FOR(i, 0, n) cout << xr[i] << ' '; cout << ENDL; //FOR(i, 0, n) cout << yr[i] << ' '; } void add(int y, int x, int t, ii s = { 0, 0 }, ii e = { MAXN-1, MAXN-1 }) { if(y < s.first || e.first < y || x < s.second || e.second < x) return; int my = (s.first + e.first) / 2, mx = (s.second + e.second) / 2; if((mp[{ s, e }] += t) == 0) mp.erase({ s, e }); if(s != e) { add(y, x, t, { s.first, s.second }, { my, mx }); add(y, x, t, { my+1, s.second }, { e.first, mx }); add(y, x, t, { s.first, mx+1 }, { my, e.second }); add(y, x, t, { my+1, mx+1 }, { e.first, e.second }); } } int sum(ii s, ii e, ii ns = { 0, 0 }, ii ne = { MAXN-1, MAXN-1 }) { if(mp.find({ ns, ne }) == mp.end()) return 0; if(s.first <= ns.first && ne.first <= e.first && s.second <= ns.second && ne.second <= e.second) return mp[{ ns, ne }]; if(ne.first < s.first || e.first < ns.first || ne.second < s.second || e.second < ns.second) return 0; int my = (ns.first + ne.first) / 2, mx = (ns.second + ne.second) / 2; return sum(s, e, ns, { my, mx }) + sum(s, e, { ns.first, mx+1 }, { my, ne.second }) + sum(s, e, { my+1, ns.second }, { ne.first, mx }) + sum(s, e, { my+1, mx+1 }, { ne.first, ne.second }); } int solve() { FOR(i, 0, n) add(xr[i], yr[i], 1); while(qq--) { int tt; tt = sc.r(); if(tt == 1) { int sy, sx, ey, ex; sy = sc.r(), ey = sc.r(), sx = sc.r(), ex = sc.r(); --sy, --sx, --ey, --ex; //debug(sy, sx, ey, ex); cout << sum({ sy, sx }, { ey, ex }) << ENDL; } else { int a, b; a = sc.r(), b = sc.r(); a = yidx[a-1], b = yidx[b-1]; add(xr[a], yr[b], 1), add(xr[b], yr[a], 1); add(xr[a], yr[a], -1), add(xr[b], yr[b], -1); swap(yr[a], yr[b]); swap(yidx[yr[a]], yidx[yr[b]]); assert(mp.size() < 4e6); //debug(yr[a], yr[b], yidx[yr[a]], yidx[yr[b]]); //FOR(i, 0, n) cout << xr[i] << ' '; cout << ENDL; //FOR(i, 0, n) cout << yr[i] << ' '; cout << ENDL; } } return 0; } // ................. main .................. // void execute() { input(), solve(); } int main(void) { #ifdef LOCAL_BOOKNU freopen("input.txt", "r", stdin); // freopen("out.txt", "w", stdout); #endif cin.tie(0), ios_base::sync_with_stdio(false); execute(); return 0; } // ......................................... //sparse 2D segtree를 사용한 코드 보기(set)
#include <bits/stdc++.h> #include <ext/pb_ds/assoc_container.hpp> #include <ext/pb_ds/tree_policy.hpp> using namespace std; using namespace __gnu_pbds; #ifdef LOCAL_BOOKNU #define debug(...) cerr << "[" << #__VA_ARGS__ << "]:", debug_out(__VA_ARGS__) #else #define debug(...) 42 #endif // ........................macro.......................... // #define FOR(i, f, n) for(int (i) = (f); (i) < (int)(n); ++(i)) #define RFOR(i, f, n) for(int (i) = (f); (i) >= (int)(n); --(i)) #define pb push_back #define emb emplace_back #define fi first #define se second #define ENDL '\n' #define sz(A) (int)(A).size() #define ALL(A) A.begin(), A.end() #define UNIQUE(c) (c).resize(unique(ALL(c)) - (c).begin()) #define next next9876 #define prev prev1234 typedef pair<int, int> ii; typedef pair<int, ii> iii; typedef vector<int> vi; typedef vector<vi> vvi; typedef vector<ii> vii; typedef vector<vii> vvii; typedef long long i64; typedef unsigned long long ui64; typedef tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update> treeset; // key, val, comp, implements, 노드 불변 규칙 // inline i64 GCD(i64 a, i64 b) { if(b == 0) return a; return GCD(b, a % b); } inline int getidx(const vi& ar, int x) { return lower_bound(ALL(ar), x) - ar.begin(); } // 정렬된 ar에서 x의 idx를 찾음 inline i64 GCD(i64 a, i64 b) { i64 n; if(a < b) swap(a, b); while(b != 0) { n = a % b; a = b; b = n; } return a; } inline i64 LCM(i64 a, i64 b) { if(a == 0 || b == 0) return GCD(a, b); return a / GCD(a, b) * b; } inline i64 CEIL(i64 n, i64 d) { return n / d + (i64)(n % d != 0); } // 음수일 떄 이상하게 작동할 수 있음 inline i64 ROUND(i64 n, i64 d) { return n / d + (i64)((n % d) * 2 >= d); } inline i64 POW(i64 a, i64 n) { assert(0 <= n); i64 ret; for(ret = 1; n; a = a*a, n /= 2) { if(n%2) ret *= a; } return ret; } template <class T> ostream& operator<<(ostream& os, vector<T> v) { os << "["; int cnt = 0; for(auto vv : v) { os << vv; if(++cnt < v.size()) os << ","; } return os << "]"; } template <class T> ostream& operator<<(ostream& os, set<T> v) { os << "["; int cnt = 0; for(auto vv : v) { os << vv; if(++cnt < v.size()) os << ","; } return os << "]"; } template <class L, class R> ostream& operator<<(ostream& os, pair<L, R> p) { return os << "(" << p.fi << "," << p.se << ")"; } void debug_out() { cerr << endl; } template <typename Head, typename... Tail> void debug_out(Head H, Tail... T) { cerr << " " << H, debug_out(T...); } // ....................................................... // const int MAXN = 2e5+10; struct fenwick { int n; vector<treeset> t; fenwick(int _n) : n(_n), t(n+1, treeset()) { } void add(int x, int y) { for(++x; x < t.size(); x += (x&-x)) { t[x].insert(y); } } void remove(int x, int y) { for(++x; x < t.size(); x += (x&-x)) { t[x].erase(y); } } int sum(int x, int y) { // if(x < 0 || y < 0) return 0; int ret = 0; for(++x, ++y; x > 0; x -= (x&-x)) { ret += t[x].order_of_key(y); } return ret; } int sum(int sx, int ex, int sy, int ey) { return sum(ex, ey) - sum(sx-1, ey) - sum(ex, sy-1) + sum(sx-1, sy-1); } } ft(MAXN); int n, qq, xr[MAXN], yr[MAXN], yidx[MAXN]; void input() { cin >> n >> qq; int p; FOR(i, 0, n) cin >> p, xr[p-1] = i; FOR(i, 0, n) cin >> p, yr[p-1] = i, yidx[i] = p-1; } int solve() { FOR(i, 0, n) ft.add(xr[i], yr[i]); while(qq--) { int tt; cin >> tt; if(tt == 1) { int sy, sx, ey, ex; cin >> sx >> ex >> sy >> ey; --sy, --ey, --sx, --ex; cout << ft.sum(sx, ex, sy, ey) << ENDL; } else { int a, b; cin >> a >> b; a = yidx[a-1], b = yidx[b-1]; ft.remove(xr[a], yr[a]), ft.remove(xr[b], yr[b]); ft.add(xr[a], yr[b]), ft.add(xr[b], yr[a]); swap(yr[a], yr[b]); swap(yidx[yr[a]], yidx[yr[b]]); } } return 0; } // ................. main .................. // void execute() { input(), solve(); } #ifndef LOCAL_BOOKNU int main(void) { cin.tie(0), ios_base::sync_with_stdio(false); execute(); return 0; } #endif // ......................................... //sparse 2D segtree를 사용한 코드 보기(배열)
#include <bits/stdc++.h> #define forn(i, n) for (int i = 0; i < int(n); i++) using namespace std; const int N = 200 * 1000 + 13; int n, m; int a[N], b[N], pos[N]; vector<int> f[N]; vector<int> vals[N]; void addupd(int x, int y){ for (int i = x; i < N; i |= i + 1) vals[i].push_back(y); } void addget(int x, int y){ if (x < 0 || y < 0) return; for (int i = x; i >= 0; i = (i & (i + 1)) - 1) vals[i].push_back(y); } void upd(int x, int y, int val){ for (int i = x; i < N; i |= i + 1) for (int j = lower_bound(vals[i].begin(), vals[i].end(), y) - vals[i].begin(); j < int(f[i].size()); j |= j + 1) f[i][j] += val; } int get(int x, int y){ if (x < 0 || y < 0) return 0; int res = 0; for (int i = x; i >= 0; i = (i & (i + 1)) - 1) for (int j = lower_bound(vals[i].begin(), vals[i].end(), y) - vals[i].begin(); j >= 0; j = (j & (j + 1)) - 1) res += f[i][j]; return res; } struct query{ int t, la, ra, lb, rb; query(){}; }; query q[N]; int main() { scanf("%d%d", &n, &m); forn(i, n){ scanf("%d", &a[i]); --a[i]; pos[a[i]] = i; } forn(i, n){ scanf("%d", &b[i]); --b[i]; b[i] = pos[b[i]]; } forn(i, m){ scanf("%d", &q[i].t); if (q[i].t == 1){ scanf("%d%d%d%d", &q[i].la, &q[i].ra, &q[i].lb, &q[i].rb); --q[i].la, --q[i].ra, --q[i].lb, --q[i].rb; } else{ scanf("%d%d", &q[i].lb, &q[i].rb); --q[i].lb, --q[i].rb; } } vector<int> tmp(b, b + n); forn(i, n) addupd(i, b[i]); forn(i, m){ if (q[i].t == 1){ addget(q[i].rb, q[i].ra); addget(q[i].lb - 1, q[i].ra); addget(q[i].rb, q[i].la - 1); addget(q[i].lb - 1, q[i].la - 1); } else{ addupd(q[i].lb, b[q[i].lb]); addupd(q[i].rb, b[q[i].rb]); swap(b[q[i].lb], b[q[i].rb]); addupd(q[i].lb, b[q[i].lb]); addupd(q[i].rb, b[q[i].rb]); } } forn(i, n) b[i] = tmp[i]; forn(i, N){ sort(vals[i].begin(), vals[i].end()); vals[i].resize(unique(vals[i].begin(), vals[i].end()) - vals[i].begin()); f[i].resize(vals[i].size(), 0); } forn(i, n) upd(i, b[i], 1); forn(i, m){ if (q[i].t == 1){ int res = 0; res += get(q[i].rb, q[i].ra); res -= get(q[i].lb - 1, q[i].ra); res -= get(q[i].rb, q[i].la - 1); res += get(q[i].lb - 1, q[i].la - 1); printf("%d\n", res); } else{ upd(q[i].lb, b[q[i].lb], -1); upd(q[i].rb, b[q[i].rb], -1); swap(b[q[i].lb], b[q[i].rb]); upd(q[i].lb, b[q[i].lb], 1); upd(q[i].rb, b[q[i].rb], 1); } } return 0; }후기
E번에서 “
2D SegTree는segtree안에segtree를 넣어야 돼서 공간복잡도가 $O(n^2)$이다.” 라는 고정관념 때문에 그 안에set을 넣는다는 생각을 하지 못했다.문제 압축까지 다 하고 QuadTree로 열심히 구현했으나 TLE가 난게 아쉽다.
-
백준 BOJ 1722 순열의 순서
문제
BOJ 1722(https://www.acmicpc.net/problem/1722)
$\lbrace 1, 2, 3, 4, … , n \rbrace$을 시작으로 하는 순열이 있다.
현재 순열의 상태에서 다음 순열의 상태로 가는 연산이
C++의next_permutation과 같이 동작 할 때 해당 순열이 몇 번째인지, 혹은 $k$번째 순열이 무엇인지 구해야한다.풀이
순열을 각 자리로 쪼개서 생각해보자.
현재 순열에서 $i$번째 자리의 숫자가 $1$단계 증가하려면 몇 번의 순열 증가 연산을 거쳐야 할까?
(이 때 $1$단계 증가한다는 것은 단순히 숫자가 1 증가한다는 것이 아니라 $A[1..i)$와 $A(i..n]$ 각각의 순서 관계는 변함 없이 순수하게 $A[i]$만 한 단계 상승하는 것을 의미한다.
예를 들어, $\lbrace 2, 1, 3, 4 \rbrace$가 있으면 $i = 2$일 때 $\lbrace 2, 3, 1, 4 \rbrace$로 증가하는 것을 의미한다.)
이 경우는 당연히 $i$번째 이전 자리는 건들 필요가 없으니 $i$이후의 자리가 몇 번이나 바뀌는지를 봐야 하는데, $(n-i)!$만큼의 연산이 필요하다는 것을 알 수 있다.
따라서 $k$번째 순열을 알아야 한다면 초기 수열에서 시작해 가장 앞의 자리수부터 k이하의 되는 선에서 최대한 증가시키는 것을 반복해나가면 된다.
또한 $A$가 몇 번째 순열인지 알아내는 것도 마찬가지로 가장 앞의 자리수부터 이 자리수가 몇 번이나 증가된 것인지를 알아내어 더해가는 것을 반복하면 된다.
(이 때, $k$가 $1$-indexed 라는 것에 주의해서 구현해야 한다.)
소스코드
#include <bits/stdc++.h> using namespace std; #ifdef LOCAL_BOOKNU #define debug(...) cerr << "[" << #__VA_ARGS__ << "]:", debug_out(__VA_ARGS__) #else #define debug(...) 42 #endif // ........................macro.......................... // #define FOR(i, f, n) for(int (i) = (f); (i) < (int)(n); ++(i)) #define RFOR(i, f, n) for(int (i) = (f); (i) >= (int)(n); --(i)) #define pb push_back #define emb emplace_back #define fi first #define se second #define ENDL '\n' #define sz(A) (int)(A).size() #define ALL(A) A.begin(), A.end() #define UNIQUE(c) (c).resize(unique(ALL(c)) - (c).begin()) #define next next9876 #define prev prev1234 typedef pair<int, int> ii; typedef pair<int, ii> iii; typedef vector<int> vi; typedef vector<vi> vvi; typedef vector<ii> vii; typedef vector<vii> vvii; typedef long long i64; typedef unsigned long long ui64; // inline i64 GCD(i64 a, i64 b) { if(b == 0) return a; return GCD(b, a % b); } inline int getidx(const vi& ar, int x) { return lower_bound(ALL(ar), x) - ar.begin(); } // 좌표 압축에 사용: 정렬된 ar에서 x의 idx를 찾음 inline i64 GCD(i64 a, i64 b) { i64 n; if(a < b) swap(a, b); while(b != 0) { n = a % b; a = b; b = n; } return a; } inline i64 LCM(i64 a, i64 b) { if(a == 0 || b == 0) return GCD(a, b); return a / GCD(a, b) * b; } inline i64 CEIL(i64 n, i64 d) { return n / d + (i64)(n % d != 0); } // 음수일 때 이상하게 작동할 수 있음. inline i64 ROUND(i64 n, i64 d) { return n / d + (i64)((n % d) * 2 >= d); } inline i64 POW(i64 a, i64 n) { assert(0 <= n); i64 ret; for(ret = 1; n; a = a*a, n /= 2) { if(n%2) ret *= a; } return ret; } template <class T> ostream& operator<<(ostream& os, vector<T> v) { os << "["; int cnt = 0; for(auto vv : v) { os << vv; if(++cnt < v.size()) os << ","; } return os << "]"; } template <class T> ostream& operator<<(ostream& os, set<T> v) { os << "["; int cnt = 0; for(auto vv : v) { os << vv; if(++cnt < v.size()) os << ","; } return os << "]"; } template <class L, class R> ostream& operator<<(ostream& os, pair<L, R> p) { return os << "(" << p.fi << "," << p.se << ")"; } void debug_out() { cerr << endl; } template <typename Head, typename... Tail> void debug_out(Head H, Tail... T) { cerr << " " << H, debug_out(T...); } // ....................................................... // int n; i64 f[21]; vi ar, rem; void input() { cin >> n; } int solve() { f[0] = 1; FOR(i, 1, 21) f[i] = f[i-1] * i; FOR(i, 0, n) rem.pb(i+1); int tt; cin >> tt; if(tt == 1) { i64 k; cin >> k; --k; FOR(i, 0, n) { ar.pb(rem[k/f[n-i-1]]); rem.erase(rem.begin() + k/f[n-i-1]); k %= f[n-i-1]; } FOR(i, 0, n) cout << ar[i] << ' '; cout << ENDL; } else { ar.resize(n); FOR(i, 0, n) cin >> ar[i]; i64 ans = 1; FOR(i, 0, n) { auto it = lower_bound(ALL(rem), ar[i]); ans += f[n-i-1] * (it-rem.begin()); rem.erase(it); } cout << ans << ENDL; } return 0; } // ................. main .................. // void execute() { input(), solve(); } int main(void) { #ifdef LOCAL_BOOKNU freopen("input.txt", "r", stdin); // freopen("out.txt", "w", stdout); #endif cin.tie(0), ios_base::sync_with_stdio(false); execute(); return 0; } // ......................................... //
-
코드포스 Codeforces Round #530(Div.2)(Virtual) 리뷰 - 모닝코포
개요
전반적으로 난이도가 괜찮았다.
실수 몇 번만 아니었으면 더 좋았을 것 같다.
A번
A번 문제:
구현현재 무게가 $w$인 눈덩이가 $h$ 높이의 비탈길에서 굴러떨어진다.
또한 비탈길 중간 $d_i$높이에서 $u_i$무게를 가진 돌 $2$개가 존재한다.
눈덩이는 매 높이마다 $1$의 높이만큼 떨어지는데, 그 때마다 떨어지기 이전 높이 $h$만큼 무게가 늘어난다.
그러다가 중간에 돌을 만나면, $d_i$만큼 눈덩이의 무게가 줄며, 만약 그 결과가 음수이면 눈덩이의 무게는 0에서부터 다시 불어나야 한다.
이 때 눈덩이의 최종 무게는?
풀이 보기
단순 구현문제이다.
위에서 서술한 그대로 구현하면 된다.
소스코드 보기
#include <bits/stdc++.h> using namespace std; #ifdef LOCAL_BOOKNU #define debug(...) cerr << "[" << #__VA_ARGS__ << "]:", debug_out(__VA_ARGS__) #else #define debug(...) 42 #endif // ........................macro.......................... // #define FOR(i, f, n) for(int (i) = (f); (i) < (int)(n); ++(i)) #define RFOR(i, f, n) for(int (i) = (f); (i) >= (int)(n); --(i)) #define pb push_back #define emb emplace_back #define fi first #define se second #define ENDL '\n' #define sz(A) (int)(A).size() #define ALL(A) A.begin(), A.end() #define UNIQUE(c) (c).resize(unique(ALL(c)) - (c).begin()) #define next next9876 #define prev prev1234 typedef pair<int, int> ii; typedef pair<int, ii> iii; typedef vector<int> vi; typedef vector<vi> vvi; typedef vector<ii> vii; typedef vector<vii> vvii; typedef long long i64; typedef unsigned long long ui64; // inline i64 GCD(i64 a, i64 b) { if(b == 0) return a; return GCD(b, a % b); } inline int getidx(const vi& ar, int x) { return lower_bound(ALL(ar), x) - ar.begin(); } // 좌표 압축에 사용: 정렬된 ar에서 x의 idx를 찾음 inline i64 GCD(i64 a, i64 b) { i64 n; if(a < b) swap(a, b); while(b != 0) { n = a % b; a = b; b = n; } return a; } inline i64 LCM(i64 a, i64 b) { if(a == 0 || b == 0) return GCD(a, b); return a / GCD(a, b) * b; } inline i64 CEIL(i64 n, i64 d) { return n / d + (i64)(n % d != 0); } // 음수일 때 이상하게 작동할 수 있음. inline i64 ROUND(i64 n, i64 d) { return n / d + (i64)((n % d) * 2 >= d); } inline i64 POW(i64 a, i64 n) { assert(0 <= n); i64 ret; for(ret = 1; n; a = a*a, n /= 2) { if(n%2) ret *= a; } return ret; } template <class T> ostream& operator<<(ostream& os, vector<T> v) { os << "["; int cnt = 0; for(auto vv : v) { os << vv; if(++cnt < v.size()) os << ","; } return os << "]"; } template <class T> ostream& operator<<(ostream& os, set<T> v) { os << "["; int cnt = 0; for(auto vv : v) { os << vv; if(++cnt < v.size()) os << ","; } return os << "]"; } template <class L, class R> ostream& operator<<(ostream& os, pair<L, R> p) { return os << "(" << p.fi << "," << p.se << ")"; } void debug_out() { cerr << endl; } template <typename Head, typename... Tail> void debug_out(Head H, Tail... T) { cerr << " " << H, debug_out(T...); } // ....................................................... // int w, h, h1, h2, d1, d2; void input() { cin >> w >> h >> d1 >> h1 >> d2 >> h2; } int solve() { while(h) { w += h; if(h == h1) w = max(0, w-d1); if(h == h2) w = max(0, w-d2); --h; } cout << w << ENDL; return 0; } // ................. main .................. // void execute() { input(), solve(); } int main(void) { #ifdef LOCAL_BOOKNU freopen("input.txt", "r", stdin); // freopen("out.txt", "w", stdout); #endif cin.tie(0), ios_base::sync_with_stdio(false); execute(); return 0; } // ......................................... //B번
B번 문제:
구현그리디Math$n$개의 정사각형을 그리려고 한다.
이 때, 현재 그리려는 선분과 평행하면서 같은 $x$좌표 범위 혹은 같은 $y$좌표 범위에 있는 선분이 이미 그려져있다면 코스트 없이 선분을 그릴 수 있다.
또한 코스트가 필요할 경우는 직사각형의 한 변과 같은 길이의 선분을 그릴 때 $1$만큼 필요하다.
이 때 $n$개의 정사각형을 그리기 위해 필요한 최소 코스트는?
예를 들어 $2$개의 정사각형을 그릴 때는 아래와 같이 빨간색 선분 3개에 대해서만 코스트를 지불하면 된다.

풀이 보기
그리디하게 생각하면 $w \cdot h$ 범위 내에 정사각형을 채우는 경우는 $w+h$코스트만을 지불하면 된다.
즉, 가장 겉 선분의 코스트만을 지불하면 되는 것이다.
그렇다면 $n$개의 사각형을 $w \cdot h$범위 내에 채우는 가장 효율적인 방법은 무엇일까?
우리는 두 수를 곱할 때 수의 합이 같을 경우 최대한 비슷한 수를 곱하는 것이 가장 큰 값이 된다는 것을 알고 있다.
이것을 그대로 적용하면 $w=h$이거나 $w=h+1$인 경우에 같은 $w+h$를 갖는 경우 중 두 수의 곱이 가장 커지게 된다는 것을 알 수 있다.
따라서 $n \leq w \cdot h$인 $w$, $h$ 중 가장 작은 $w+h$를 위와 같은 방식으로 구하면 된다.
소스코드 보기
#include <bits/stdc++.h> using namespace std; #ifdef LOCAL_BOOKNU #define debug(...) cerr << "[" << #__VA_ARGS__ << "]:", debug_out(__VA_ARGS__) #else #define debug(...) 42 #endif // ........................macro.......................... // #define FOR(i, f, n) for(int (i) = (f); (i) < (int)(n); ++(i)) #define RFOR(i, f, n) for(int (i) = (f); (i) >= (int)(n); --(i)) #define pb push_back #define emb emplace_back #define fi first #define se second #define ENDL '\n' #define sz(A) (int)(A).size() #define ALL(A) A.begin(), A.end() #define UNIQUE(c) (c).resize(unique(ALL(c)) - (c).begin()) #define next next9876 #define prev prev1234 typedef pair<int, int> ii; typedef pair<int, ii> iii; typedef vector<int> vi; typedef vector<vi> vvi; typedef vector<ii> vii; typedef vector<vii> vvii; typedef long long i64; typedef unsigned long long ui64; // inline i64 GCD(i64 a, i64 b) { if(b == 0) return a; return GCD(b, a % b); } inline int getidx(const vi& ar, int x) { return lower_bound(ALL(ar), x) - ar.begin(); } // 좌표 압축에 사용: 정렬된 ar에서 x의 idx를 찾음 inline i64 GCD(i64 a, i64 b) { i64 n; if(a < b) swap(a, b); while(b != 0) { n = a % b; a = b; b = n; } return a; } inline i64 LCM(i64 a, i64 b) { if(a == 0 || b == 0) return GCD(a, b); return a / GCD(a, b) * b; } inline i64 CEIL(i64 n, i64 d) { return n / d + (i64)(n % d != 0); } // 음수일 때 이상하게 작동할 수 있음. inline i64 ROUND(i64 n, i64 d) { return n / d + (i64)((n % d) * 2 >= d); } inline i64 POW(i64 a, i64 n) { assert(0 <= n); i64 ret; for(ret = 1; n; a = a*a, n /= 2) { if(n%2) ret *= a; } return ret; } template <class T> ostream& operator<<(ostream& os, vector<T> v) { os << "["; int cnt = 0; for(auto vv : v) { os << vv; if(++cnt < v.size()) os << ","; } return os << "]"; } template <class T> ostream& operator<<(ostream& os, set<T> v) { os << "["; int cnt = 0; for(auto vv : v) { os << vv; if(++cnt < v.size()) os << ","; } return os << "]"; } template <class L, class R> ostream& operator<<(ostream& os, pair<L, R> p) { return os << "(" << p.fi << "," << p.se << ")"; } void debug_out() { cerr << endl; } template <typename Head, typename... Tail> void debug_out(Head H, Tail... T) { cerr << " " << H, debug_out(T...); } // ....................................................... // i64 x; void input() { cin >> x; } int solve() { i64 w = 1, h = 1; while(w*h < x) { ++h; if(w < h) swap(w, h); } cout << w+h << ENDL; return 0; } // ................. main .................. // void execute() { input(), solve(); } int main(void) { #ifdef LOCAL_BOOKNU freopen("input.txt", "r", stdin); // freopen("out.txt", "w", stdout); #endif cin.tie(0), ios_base::sync_with_stdio(false); execute(); return 0; } // ......................................... //후기
처음에는 $n$의 두 약수 $a$, $b$ 중 $a + b$가 가장 작은 경우를 찾으면 되는줄 알고 한 번 틀렸다.
B번이라고 너무 생각없이 풀었는데, 이런 사소한 실수도 조심해야겠다.
C번
C번 문제:
구현그리디문자열이 하나 주어지고, 해당 문자열에는 특수 문자 두 가지가 들어가있다.
각 특수문자의 앞에는 무조건 일반 문자가 존재한다.
$?$ : 앞의 문자를 지우거나 남겨둘 수 있다.
$*$ : 앞의 문자를 지우거나 $0$번 이상 반복시킬 수 있다.
특수 문자 연산을 적절히 하여 길이가 $k$인 문자열로 만들 수 있을까?
만들 수 있는 경우 해당 문자열을 출력해야 한다.
풀이 보기
단순하게 생각하자.
결과 문자열이 어떻든 상관 없이 길이만 맞추면 된다.
일반문자의 수를 $n$, $?$의 수를 $a$, $*$의 수를 $b$이라고 할 때, 우리가 만들 수 있는 문자열의 길이의 범위는 어떻게 될까?
따라서 만들 문자열 $k$가 위의 범위에 들어가는 경우 결과를 출력하도록 구현만 하면 된다.
급하게 짜느라 구현이 좀 더러워졌는데, 조금만 고치면 더 깔끔하게 구현도 가능 할 것 같다.
소스코드 보기
#include <bits/stdc++.h> using namespace std; #ifdef LOCAL_BOOKNU #define debug(...) cerr << "[" << #__VA_ARGS__ << "]:", debug_out(__VA_ARGS__) #else #define debug(...) 42 #endif // ........................macro.......................... // #define FOR(i, f, n) for(int (i) = (f); (i) < (int)(n); ++(i)) #define RFOR(i, f, n) for(int (i) = (f); (i) >= (int)(n); --(i)) #define pb push_back #define emb emplace_back #define fi first #define se second #define ENDL '\n' #define sz(A) (int)(A).size() #define ALL(A) A.begin(), A.end() #define UNIQUE(c) (c).resize(unique(ALL(c)) - (c).begin()) #define next next9876 #define prev prev1234 typedef pair<int, int> ii; typedef pair<int, ii> iii; typedef vector<int> vi; typedef vector<vi> vvi; typedef vector<ii> vii; typedef vector<vii> vvii; typedef long long i64; typedef unsigned long long ui64; // inline i64 GCD(i64 a, i64 b) { if(b == 0) return a; return GCD(b, a % b); } inline int getidx(const vi& ar, int x) { return lower_bound(ALL(ar), x) - ar.begin(); } // 좌표 압축에 사용: 정렬된 ar에서 x의 idx를 찾음 inline i64 GCD(i64 a, i64 b) { i64 n; if(a < b) swap(a, b); while(b != 0) { n = a % b; a = b; b = n; } return a; } inline i64 LCM(i64 a, i64 b) { if(a == 0 || b == 0) return GCD(a, b); return a / GCD(a, b) * b; } inline i64 CEIL(i64 n, i64 d) { return n / d + (i64)(n % d != 0); } // 음수일 때 이상하게 작동할 수 있음. inline i64 ROUND(i64 n, i64 d) { return n / d + (i64)((n % d) * 2 >= d); } inline i64 POW(i64 a, i64 n) { assert(0 <= n); i64 ret; for(ret = 1; n; a = a*a, n /= 2) { if(n%2) ret *= a; } return ret; } template <class T> ostream& operator<<(ostream& os, vector<T> v) { os << "["; int cnt = 0; for(auto vv : v) { os << vv; if(++cnt < v.size()) os << ","; } return os << "]"; } template <class T> ostream& operator<<(ostream& os, set<T> v) { os << "["; int cnt = 0; for(auto vv : v) { os << vv; if(++cnt < v.size()) os << ","; } return os << "]"; } template <class L, class R> ostream& operator<<(ostream& os, pair<L, R> p) { return os << "(" << p.fi << "," << p.se << ")"; } void debug_out() { cerr << endl; } template <typename Head, typename... Tail> void debug_out(Head H, Tail... T) { cerr << " " << H, debug_out(T...); } // ....................................................... // string s; int n, k; void input() { cin >> s >> k; n = s.size(); } int solve() { int ca = 0, sn = 0; FOR(i, 0, n) { if(s[i] == '?') ++ca; if(s[i] == '*') ++sn; } n -= (ca+sn); if(!(n-ca-sn <= k && (k <= n || sn))) { cout << "Impossible" << ENDL; return 0; } int inc = 0, rem = 0; if(k > n) inc = k-n; if(k < n) rem = n-k; debug(inc, rem); string ans; FOR(i, 0, s.size()) { if(s[i] != '*' && s[i] != '?') ans.pb(s[i]); else if(inc && s[i] == '*') { FOR(j, 0, inc) ans.pb(s[i-1]); inc = 0; } else if(rem && (s[i] == '?' || s[i] == '*')) { ans.pop_back(); rem--; } } cout << ans << ENDL; return 0; } // ................. main .................. // void execute() { input(), solve(); } int main(void) { #ifdef LOCAL_BOOKNU freopen("input.txt", "r", stdin); // freopen("out.txt", "w", stdout); #endif cin.tie(0), ios_base::sync_with_stdio(false); execute(); return 0; } // ......................................... //D번
D번 문제:
트리그리디$n$개의 정점을 가진 트리가 있고, 각 정점에는 가중치 $a_i$가 부여 되어있다.
$s_u = sum(a_{u \in path(root, u)})$라고 정의된다.
트리에서 홀수 깊이($root$의 깊이 = 1) 정점의 $s_i$만을 알 수 있을 때 이런 경우가 가능한지, 가능한 경우 중 $a_i$의 합이 가장 작은 경우를 찾아야 한다.
풀이 보기
직관적으로 생각했을 때 최대한 트리의 상위 노드의 $a_i$를 크게 부여하는 것이 무조건 이득이라는 것을 알 수 있다.
따라서 $root$에서부터
Top-Down방식으로 $a_i$를 부여해나가면 된다.이 때, 하위 노드에서 현재까지 $s_{par[u]}$가 어느만큼 채워졌는지에 대한 정보를 인자로 넘겨주면 편하다.
또한 현재 노드가 짝수 깊이의 노드여서 $s_u$가 특정되지 않았다면 $min(s_{v \in child[u]})$값을 채우도록 하면 된다.
불가능한지 여부는 상위 노드의 $s_u$가 하위 노드보다 작은 경우가 있는지에 대한 판단만 하면 된다.
소스코드 보기
#include <bits/stdc++.h> using namespace std; #ifdef LOCAL_BOOKNU #define debug(...) cerr << "[" << #__VA_ARGS__ << "]:", debug_out(__VA_ARGS__) #else #define debug(...) 42 #endif // ........................macro.......................... // #define FOR(i, f, n) for(int (i) = (f); (i) < (int)(n); ++(i)) #define RFOR(i, f, n) for(int (i) = (f); (i) >= (int)(n); --(i)) #define pb push_back #define emb emplace_back #define fi first #define se second #define ENDL '\n' #define sz(A) (int)(A).size() #define ALL(A) A.begin(), A.end() #define UNIQUE(c) (c).resize(unique(ALL(c)) - (c).begin()) #define next next9876 #define prev prev1234 typedef pair<int, int> ii; typedef pair<int, ii> iii; typedef vector<int> vi; typedef vector<vi> vvi; typedef vector<ii> vii; typedef vector<vii> vvii; typedef long long i64; typedef unsigned long long ui64; // inline i64 GCD(i64 a, i64 b) { if(b == 0) return a; return GCD(b, a % b); } inline int getidx(const vi& ar, int x) { return lower_bound(ALL(ar), x) - ar.begin(); } // 좌표 압축에 사용: 정렬된 ar에서 x의 idx를 찾음 inline i64 GCD(i64 a, i64 b) { i64 n; if(a < b) swap(a, b); while(b != 0) { n = a % b; a = b; b = n; } return a; } inline i64 LCM(i64 a, i64 b) { if(a == 0 || b == 0) return GCD(a, b); return a / GCD(a, b) * b; } inline i64 CEIL(i64 n, i64 d) { return n / d + (i64)(n % d != 0); } // 음수일 때 이상하게 작동할 수 있음. inline i64 ROUND(i64 n, i64 d) { return n / d + (i64)((n % d) * 2 >= d); } inline i64 POW(i64 a, i64 n) { assert(0 <= n); i64 ret; for(ret = 1; n; a = a*a, n /= 2) { if(n%2) ret *= a; } return ret; } template <class T> ostream& operator<<(ostream& os, vector<T> v) { os << "["; int cnt = 0; for(auto vv : v) { os << vv; if(++cnt < v.size()) os << ","; } return os << "]"; } template <class T> ostream& operator<<(ostream& os, set<T> v) { os << "["; int cnt = 0; for(auto vv : v) { os << vv; if(++cnt < v.size()) os << ","; } return os << "]"; } template <class L, class R> ostream& operator<<(ostream& os, pair<L, R> p) { return os << "(" << p.fi << "," << p.se << ")"; } void debug_out() { cerr << endl; } template <typename Head, typename... Tail> void debug_out(Head H, Tail... T) { cerr << " " << H, debug_out(T...); } // ....................................................... // const int MAXN = 1e5; const i64 INF = 0x3fffffffffffffff; i64 n, ans, ar[MAXN], par[MAXN], ok; vi g[MAXN]; void input() { cin >> n; FOR(i, 1, n) cin >> par[i], g[--par[i]].pb(i); FOR(i, 0, n) cin >> ar[i]; } void f(int u, i64 p) { if(ar[u] != -1) { if(ar[u] < p) { ok = -1; return; } else { ans += (ar[u]-p); p = ar[u]; } } else if(g[u].size()) { i64 sel = INF; for(int v : g[u]) sel = min(sel, ar[v]); if(p > sel) { ok = -1; return; } ans += (sel-p); p = sel; } for(int v : g[u]) f(v, p); } int solve() { f(0, 0); if(ok == -1) cout << -1 << ENDL; else cout << ans << ENDL; return 0; } // ................. main .................. // void execute() { input(), solve(); } int main(void) { #ifdef LOCAL_BOOKNU freopen("input.txt", "r", stdin); // freopen("out.txt", "w", stdout); #endif cin.tie(0), ios_base::sync_with_stdio(false); execute(); return 0; } // ......................................... //후기
정신줄을 놓고 코딩했는지, 별로 생각을 안 하다가 바로 코딩을 해서 그런지는 모르겠지만 첫 번째 구현 때 식수로 $s_u$가 특정되지 않았을 경우에 대한 처리를 하지 않아서 한 번 틀렸다.
또한 내가 문제를 풀 때는 짝수 노드들에만 $s_u$가 특정되지 않았다는 것을 미처 보지 못했는데, 이 정보를 활용하면 아주 깔끔하게 구현 할 수 있을 것이다.
E번
E번 문제:
constructive algorithm그리디Math$n \times m$의 $A, G, C, T$로 이루어진 맵이 주어진다.
이 맵의 각 셀의 원소를 적절히 바꾸어 모든 $2 \times 2$의 부분 맵에 대하여 각 셀이 서로 다른 원소를 가지도록 만들 때, 최소 변경 수를 구하면 된다.
나는 이 문제가
DP인줄알고 열심히 점화식을 세웠지만, 결국 풀지는 못했다.튜토리얼을 보니 한 줄(row, col)에 최대 2개의 문자만이 들어가도록 맵을 바꾸는게 무조건 이득이라고 한다.
즉, 다음과 같은 형태인 경우 중 하나가 무조건 최적이라는 뜻이다.
AGAGAGAG CTCTCTCT ...왜 이렇게 되는지는 튜토리얼 페이지가 없다고 설명을 안 해줬다..;
개인적으로는
DP로도 해결 할 수 있을 것 같은데, 조금 더 생각을 해봐야겠다.후기
B, D를 실수한 것 빼고는 딱히 감흥이 없는 라운드였다.
D번도 너무 전형적인 트리 문제라 식상했던 것 같다.
E번을
DP로 풀지 못한게 약간 아쉽다.