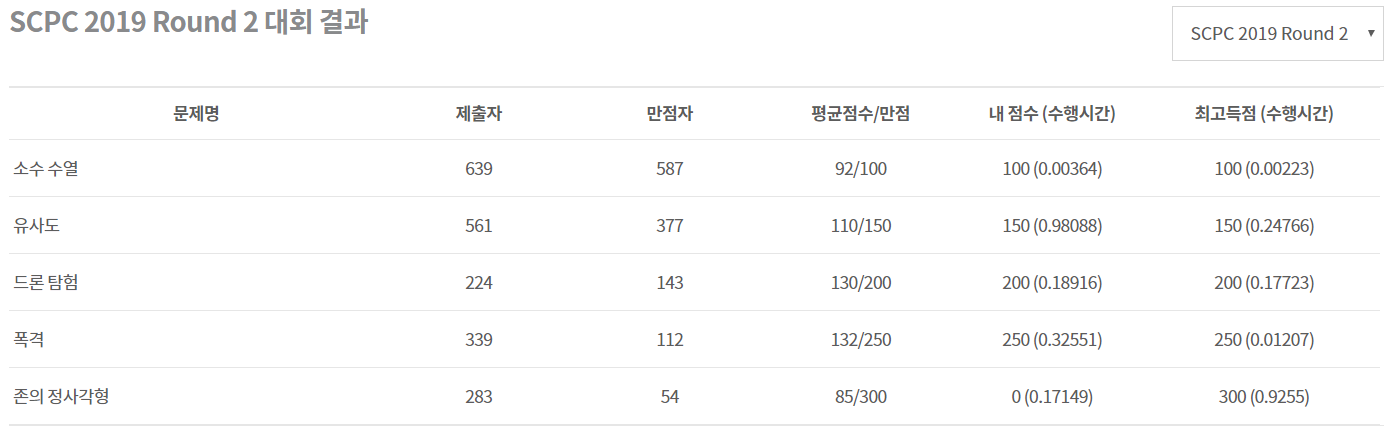
1번
DP 완전탐색
현재 숫자에서 각 자리수를 지워나갈 때, 숫자가 소수를 유지하며 지워지는 최대 횟수를 점수로 볼 때, 두 숫자의 점수를 비교하는 문제이다.
풀이 보기
문제 자체가 겉으로 보기에는 상당히 복잡해보인다.
단순하게 생각하면 각 자리를 지워보며 소수가 유지되는 최대값을 찾아가는 완전 탐색으로 풀 수 있다.
다섯 자리밖에 안 되는 숫자이기 때문에 완전 탐색으로도 시간초과가 나지 않겠지만, DP를 쓰면 더 안정적인 시간복잡도로 답을 구할 수 있을 것이다.
각 숫자를 상태공간으로 보고 해당 숫자에서 각 자리수를 지워나가며 재귀를 돌면 답을 구할 수 있다.
숫자의 각 자리를 지우는게 좀 귀찮긴 하지만, 이것은 다양한 방법으로 구현할 수 있다.
소스코드 보기
#include <bits/stdc++.h>
using namespace std;
#ifdef LOCAL_BOOKNU
#define debug(...) cerr << "[" << #__VA_ARGS__ << "]:", debug_out(__VA_ARGS__)
#else
#define debug(...) 42
#endif
// ........................macro.......................... //
#define FOR(i, f, n) for(int (i) = (f); (i) < (int)(n); ++(i))
#define RFOR(i, f, n) for(int (i) = (f); (i) >= (int)(n); --(i))
#define pb push_back
#define emb emplace_back
#define fi first
#define se second
#define ENDL '\n'
#define sz(A) (int)(A).size()
#define ALL(A) A.begin(), A.end()
#define UNIQUE(c) (c).resize(unique(ALL(c)) - (c).begin())
#define next next9876
#define prev prev1234
typedef pair<int, int> ii;
typedef pair<int, ii> iii;
typedef vector<int> vi;
typedef vector<vi> vvi;
typedef vector<ii> vii;
typedef vector<vii> vvii;
typedef long long i64;
typedef unsigned long long ui64;
// inline i64 GCD(i64 a, i64 b) { if(b == 0) return a; return GCD(b, a % b); }
inline int getidx(const vi& ar, int x) { return lower_bound(ALL(ar), x) - ar.begin(); } // 좌표 압축에 사용: 정렬된 ar에서 x의 idx를 찾음
inline i64 GCD(i64 a, i64 b) { i64 n; if(a < b) swap(a, b); while(b != 0) { n = a % b; a = b; b = n; } return a; }
inline i64 LCM(i64 a, i64 b) { if(a == 0 || b == 0) return GCD(a, b); return a / GCD(a, b) * b; }
inline i64 CEIL(i64 n, i64 d) { return n / d + (i64)(n % d != 0); } // 음수일 때 이상하게 작동할 수 있음.
inline i64 ROUND(i64 n, i64 d) { return n / d + (i64)((n % d) * 2 >= d); }
const i64 MOD = 1e9+7;
inline i64 POW(i64 a, i64 n) {
assert(0 <= n);
i64 ret;
for(ret = 1; n; a = a*a%MOD, n /= 2) { if(n%2) ret = ret*a%MOD; }
return ret;
}
template <class T> ostream& operator<<(ostream& os, vector<T> v) {
os << "[";
int cnt = 0;
for(auto vv : v) { os << vv; if(++cnt < v.size()) os << ","; }
return os << "]";
}
template <class T> ostream& operator<<(ostream& os, set<T> v) {
os << "[";
int cnt = 0;
for(auto vv : v) { os << vv; if(++cnt < v.size()) os << ","; }
return os << "]";
}
template <class L, class R> ostream& operator<<(ostream& os, pair<L, R> p) { return os << "(" << p.fi << "," << p.se << ")"; }
void debug_out() { cerr << endl; }
template <typename Head, typename... Tail> void debug_out(Head H, Tail... T) { cerr << " " << H, debug_out(T...); }
// ....................................................... //
const int MAXN = 3e4+10;
int a, b, dp[MAXN];
// --> x*pr[j]에서 overflow 발생할 수 있음! 그러나 적당히 작은 RANGE에서는 소수 분포가 촘촘하기 때문에 발생하지 않음.
// --> RANGE 내의 소수 개수 = RANGE/ln(RANGE) --> 2e7에서 인접 소수 최대 차이 = 180, 4e6 = 140
const int RANGE = MAXN;
int pn, spf[RANGE], pr[RANGE]; // pr은 vi로 구현해도 됨. --> but 실행 시간 많이 늘어남.
void eulerSieve() {
FOR(x, 2, RANGE) {
if(!spf[x]) spf[x] = pr[pn++] = x; // x 자체가 소수이면 spf[x] = x이다.
for(int j = 0; x*pr[j] < RANGE; ++j) { // x의 소수배들에 spf[x*pr] = pr로 칠해준다. (단, pr <= spf[x])
spf[x*pr[j]] = pr[j];
if(x % pr[j] == 0) break; // 좀 더 직관적으로 if(spf[x] == pr[j])로 구현해도 되지만, 똑같은 효과를 가진 코드이다.
}
}
}
void input() {
// ---- !!! INIT GLOBAL VARIABLES !!! ---- //
// ---- Interactive Cautions : cin.tie(0), freopen(...), Case #x: ---- //
cin >> a >> b;
}
int f(int x) {
int& ret = dp[x];
if(ret != -1) return ret;
if(spf[x] != x) return ret = 0; // 소수가 아님
int cur = x, w = 1;
ret = 0;
while(cur) { // 각 자리를 지워보며 재귀
ret = max(ret, f((cur/10) * w + x % w));
cur /= 10;
w *= 10;
}
return ++ret;
}
int solve() {
if(f(a) > f(b)) cout << 1 << ENDL;
else if(f(a) < f(b)) cout << 2 << ENDL;
else cout << 3 << ENDL;
return 0;
}
// ................. main .................. //
void execute() {
memset(dp, -1, sizeof(dp));
eulerSieve();
spf[0] = -1;
int TTTT; cin >> TTTT;
FOR(tttt, 0, TTTT) {
cout << "Case #" << tttt+1 << ENDL;
input(), solve();
}
}
int main(void) {
#ifdef LOCAL_BOOKNU
// freopen("input.txt", "r", stdin);
// freopen("out.txt", "w", stdout);
#endif
cin.tie(0), ios_base::sync_with_stdio(false);
execute();
return 0;
}
// ......................................... //
2번
DP 팰린드롬 부분 합
길이가 같은 $A, B$ 수열이 있을 때, 같은 인덱스에 같은 수가 있는 수를 유사도라고 한다.
$B$수열의 일부를 한 번만 뒤집을 수 있을 때, $A, B$ 수열의 유사도의 최대값을 구해야한다.
풀이 보기
구현이 은근히 까다로운 문제이다. 우선, 가장 쉬운 아이디어로 $B$의 모든 구간을 뒤집어보고 유사도를 판단하는 방법이 있다.
하지만 이 방법은 모든 구간을 선택하는데 $n^2$, 유사도를 비교하는데 $n$번의 연산이 필요하기 때문에 $O(n^3)$의 시간복잡도를 갖고, 시간초과가 발생한다.
$B$의 $[s, e]$ 구간을 뒤집었을 때를 생각해보면, 구간의 길이가 홀수인 경우 어떤 중점을 기준으로 A와 뒤집어진 상태로 매핑된다는 것을 알 수 있다.
즉, 아래 그림과 같이 매핑된다.
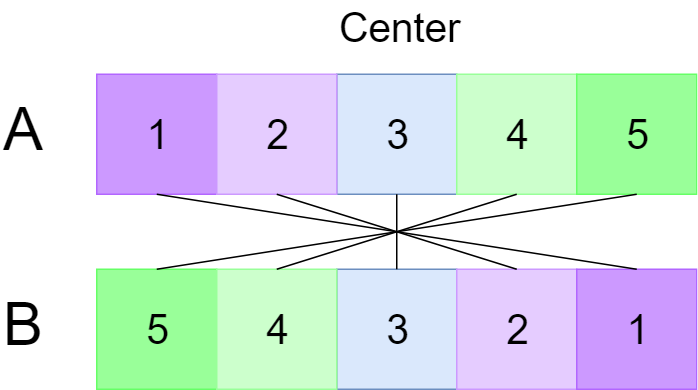
이것을 이용하면 팰린드롬의 문제처럼 구간의 길이를 점차 늘려가는 방식을 사용해 뒤집힌 구간에 대한 유사도 비교를 O(1)에 할 수 있다.
(이 때, 구현을 더 쉽게 하기 위해서 문자열 문제에서 많이 사용하는 숫자 사이에 #을 넣는 트릭을 사용할 수 있다.)
또한 뒤집히지 않은 구간에 대해서는 partial sum 아이디어를 이용하여 $[0, i]$의 유사도를 배열 형태로 저장해두면 임의의 구간에 대한 유사도 역시 $O(1)$에 구할 수 있으며, 결과적으로 모든 구간에 대해서 유사도 비교를 $O(1)$에 할 수 있으므로 시간 복잡도는 $O(n^2)$이 된다.
소스코드 보기
#include <bits/stdc++.h>
using namespace std;
#ifdef LOCAL_BOOKNU
#define debug(...) cerr << "[" << #__VA_ARGS__ << "]:", debug_out(__VA_ARGS__)
#else
#define debug(...) 42
#endif
// ........................macro.......................... //
#define FOR(i, f, n) for(int (i) = (f); (i) < (int)(n); ++(i))
#define RFOR(i, f, n) for(int (i) = (f); (i) >= (int)(n); --(i))
#define pb push_back
#define emb emplace_back
#define fi first
#define se second
#define ENDL '\n'
#define sz(A) (int)(A).size()
#define ALL(A) A.begin(), A.end()
#define UNIQUE(c) (c).resize(unique(ALL(c)) - (c).begin())
#define next next9876
#define prev prev1234
typedef pair<int, int> ii;
typedef pair<int, ii> iii;
typedef vector<int> vi;
typedef vector<vi> vvi;
typedef vector<ii> vii;
typedef vector<vii> vvii;
typedef long long i64;
typedef unsigned long long ui64;
// inline i64 GCD(i64 a, i64 b) { if(b == 0) return a; return GCD(b, a % b); }
inline int getidx(const vi& ar, int x) { return lower_bound(ALL(ar), x) - ar.begin(); } // 좌표 압축에 사용: 정렬된 ar에서 x의 idx를 찾음
inline i64 GCD(i64 a, i64 b) { i64 n; if(a < b) swap(a, b); while(b != 0) { n = a % b; a = b; b = n; } return a; }
inline i64 LCM(i64 a, i64 b) { if(a == 0 || b == 0) return GCD(a, b); return a / GCD(a, b) * b; }
inline i64 CEIL(i64 n, i64 d) { return n / d + (i64)(n % d != 0); } // 음수일 때 이상하게 작동할 수 있음.
inline i64 ROUND(i64 n, i64 d) { return n / d + (i64)((n % d) * 2 >= d); }
const i64 MOD = 1e9+7;
inline i64 POW(i64 a, i64 n) {
assert(0 <= n);
i64 ret;
for(ret = 1; n; a = a*a%MOD, n /= 2) { if(n%2) ret = ret*a%MOD; }
return ret;
}
template <class T> ostream& operator<<(ostream& os, vector<T> v) {
os << "[";
int cnt = 0;
for(auto vv : v) { os << vv; if(++cnt < v.size()) os << ","; }
return os << "]";
}
template <class T> ostream& operator<<(ostream& os, set<T> v) {
os << "[";
int cnt = 0;
for(auto vv : v) { os << vv; if(++cnt < v.size()) os << ","; }
return os << "]";
}
template <class L, class R> ostream& operator<<(ostream& os, pair<L, R> p) { return os << "(" << p.fi << "," << p.se << ")"; }
void debug_out() { cerr << endl; }
template <typename Head, typename... Tail> void debug_out(Head H, Tail... T) { cerr << " " << H, debug_out(T...); }
// ....................................................... //
const int MAXN = 5e3+1;
int n, ar[MAXN], br[MAXN], ps[MAXN], ev[MAXN], od[MAXN];
void input() {
// ---- !!! INIT GLOBAL VARIABLES !!! ---- //
cin >> n;
FOR(i, 0, n) cin >> ar[i];
FOR(i, 0, n) cin >> br[i];
memset(ps, 0, sizeof(ps));
memset(ev, 0, sizeof(ev));
}
int rs(int s, int e) {
if(s > e) return 0;
return (e < n ? ps[e] : ps[n-1]) - (s > 0 ? ps[s-1] : 0);
}
int solve() {
FOR(i, 0, n) ps[i] = (i ? ps[i-1] : 0) + (ar[i] == br[i]);
int ans = ps[n-1];
// 홀수
FOR(i, 0, n) od[i] = ar[i] == br[i];
FOR(len, 1, n) {
FOR(i, len, n-len) {
if(ar[i-len] == br[i+len]) ++od[i];
if(ar[i+len] == br[i-len]) ++od[i];
ans = max(ans, od[i] + rs(0, i-len-1) + rs(i+len+1, n-1));
}
FOR(i, len-1, n-len) {
if(ar[i+len] == br[i-len+1]) ++ev[i];
if(ar[i-len+1] == br[i+len]) ++ev[i];
ans = max(ans, ev[i] + rs(0, i-len) + rs(i+len+1, n-1));
}
}
cout << ans << ENDL;
return 0;
}
// ................. main .................. //
void execute() {
#ifdef LOCAL_BOOKNU
auto START_TIME = clock();
#endif
int TTT; cin >> TTT;
FOR(ttt, 0, TTT) cout << "Case #" << ttt+1 << ENDL,
input(), solve();
#ifdef LOCAL_BOOKNU
auto END_TIME = clock();
cout << ENDL << END_TIME - START_TIME << "ms" << ENDL;
#endif
}
int main(void) {
#ifdef LOCAL_BOOKNU
// freopen("input.txt", "r", stdin);
// freopen("out.txt", "w", stdout);
#endif
cin.tie(0), ios_base::sync_with_stdio(false);
execute();
return 0;
}
// ......................................... //
3번
그리디 기하
천장과 바닥으로 이루어진 구불구불한 도형이 주어질 때, 좌측 끝 $h_s$ 높이에서 출발하여 우측 끝 $h_e$ 높이로 최단거리로 이동할 때, 여러 최단 경로들이 나올 것이다.
(도형의 변은 $x$축 혹은 $y$축과 평행하며, 이동 역시 수평으로만 한다.)
이 때 가능한 최단 경로들을 한꺼번에 그리면 어떤 면적이 나올텐데 그 면적의 너비를 구하면 된다.
풀이 보기
도형의 전처리
우선, 이상하게 생긴 도형을 익숙하게 처리할 수 있도록 전처리를 해보자.
도형을 수직 단위로 끊으면 여러 직사각형들이 수평으로 나열된 형태가 된다.
(즉, 아래 그림과 같이 된다.)
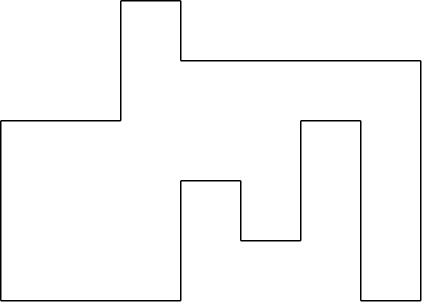
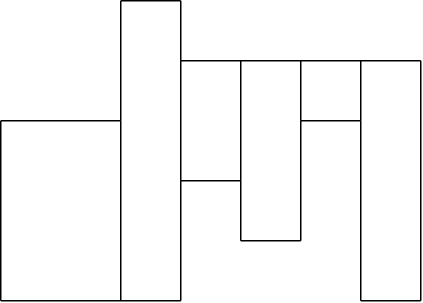
훨씬 처리하기가 편하게 변했다.
최단경로의 면적
도형이 있을 때, 다음과 같은 면적을 구하는 것이 문제의 요구사항이다.
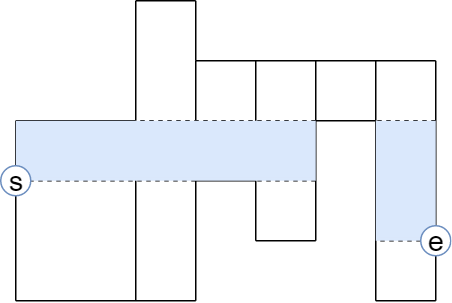
이 때 관찰할 수 있는 것은, 이 면적이 어떠한 위 껍질과, 아래 껍질로 이루어진 도형이라는 것이다.
그 껍질이 가지는 특성을 알아내면, 쉽게 면적도 알아낼 수 있을 것이다.
위 껍질의 성질
우선 아래 껍질은 제쳐두고, 위 껍질의 특성부터 알아보자.
직관적으로는 위 껍질의 특성이 도형을 위아래로 뒤집은 도형의 특성에 적용되면 아래 껍질을 구할 수 있을 것 같다는 추측을 할 수 있으므로, 위 껍질부터 알아보자.
또한, 다음 그림과 같이 일관성을 위해 시작/끝 높이에 상관 없이, 가장 왼쪽 도형의 맨 위쪽에서 시작해 가장 오른쪽 도형의 맨 위쪽으로 가는 경로들에 대해서 생각하자.
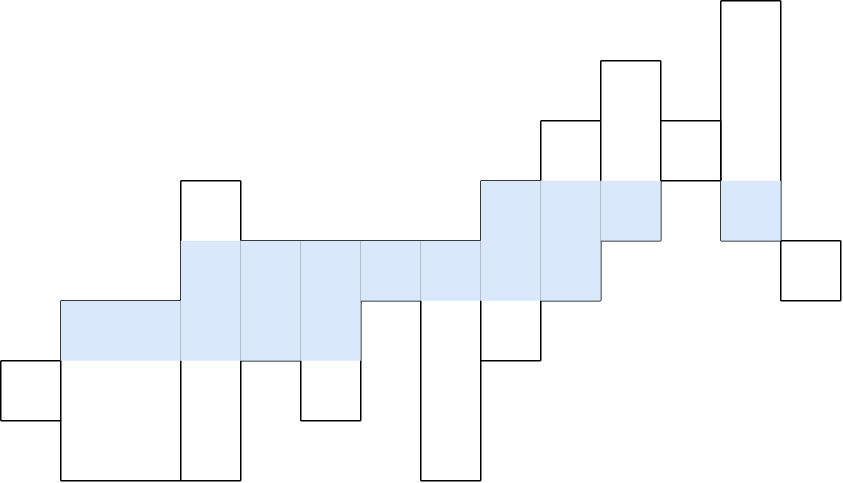
위 껍질은 가능한 최단 경로 중 최대한 위쪽을 타고 가려는 특성을 가지고 있다.
하지만, 끝 높이가 낮은 경우는 마냥 위쪽을 타고 갈 수는 없다.
그렇다고 항상 끝 높이보다 낮은 높이를 유지해야 하는 것도 아니다.
따라서 이들 사이에 관계를 찾기 위해 현재 어떤 직사각형 $i$까지 왔고, 현재 높이가 $h$이며, 현재 직사각형의 다음 직사각형 중 임의의 직사각형을 $j$라고 할 때, 이 직사각형에서는 어떤 높이를 유지해야 하는지를 알아보자.
단순히 바로 다음 직사각형만을 보고 결정할 수 없다는 것은 간단한 예제들로 알 수 있다.
그러므로 뒤의 모든 직사각형을 고려해야 하는데, 여러가지 시도를 해보면 다음과 같은 두 가지 경우가 높이를 제한한다는 것을 알 수 있다.
(설명의 편의를 위해 직사각형의 아래 높이를 $h_s$, 위 높이를 $h_e$라고 한다.)
-
높이를 높일 수 없는 경우 (상한)
$h[i]_e > h[j]_e$ 인 $j$가 존재할 경우, 현재 직사각형에서는 최대 $h[j]_e$까지 밖에 못올라간다.

-
높이를 줄일 수 없는 경우 (하한)
1번과 반대로 높이를 $x$로 줄이려고 할 때, $x < h[j]_s$ 인 $j$가 존재할 경우, 높이는 $h[j]_s$까지 밖에 줄이지 못한다.
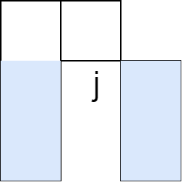
아래 껍질의 경우
위 껍질이 최대한 위를 타고 가려는 특성이 있다면, 아래 껍질 역시 최대한 아래를 다고 가려는 특성이 있다.
따라서 위 껍질을 구하는 알고리즘을 그대로 이용하면 아래 껍질 역시 쉽게 구할 수 있다.
소스코드 보기
#include <bits/stdc++.h>
using namespace std;
#ifdef LOCAL_BOOKNU
#define debug(...) cerr << "[" << #__VA_ARGS__ << "]:", debug_out(__VA_ARGS__)
#else
#define debug(...) 42
#endif
// ........................macro.......................... //
#define FOR(i, f, n) for(int (i) = (f); (i) < (int)(n); ++(i))
#define RFOR(i, f, n) for(int (i) = (f); (i) >= (int)(n); --(i))
#define pb push_back
#define emb emplace_back
#define fi first
#define se second
#define ENDL '\n'
#define sz(A) (int)(A).size()
#define ALL(A) A.begin(), A.end()
#define UNIQUE(c) (c).resize(unique(ALL(c)) - (c).begin())
#define next next9876
#define prev prev1234
typedef pair<int, int> ii;
typedef pair<int, ii> iii;
typedef vector<int> vi;
typedef vector<vi> vvi;
typedef vector<ii> vii;
typedef vector<vii> vvii;
typedef long long i64;
typedef unsigned long long ui64;
// inline i64 GCD(i64 a, i64 b) { if(b == 0) return a; return GCD(b, a % b); }
inline int getidx(const vi& ar, int x) { return lower_bound(ALL(ar), x) - ar.begin(); } // 좌표 압축에 사용: 정렬된 ar에서 x의 idx를 찾음
inline i64 GCD(i64 a, i64 b) { i64 n; if(a < b) swap(a, b); while(b != 0) { n = a % b; a = b; b = n; } return a; }
inline i64 LCM(i64 a, i64 b) { if(a == 0 || b == 0) return GCD(a, b); return a / GCD(a, b) * b; }
inline i64 CEIL(i64 n, i64 d) { return n / d + (i64)(n % d != 0); } // 음수일 때 이상하게 작동할 수 있음.
inline i64 ROUND(i64 n, i64 d) { return n / d + (i64)((n % d) * 2 >= d); }
const i64 MOD = 1e9+7;
inline i64 POW(i64 a, i64 n) {
assert(0 <= n);
i64 ret;
for(ret = 1; n; a = a*a%MOD, n /= 2) { if(n%2) ret = ret*a%MOD; }
return ret;
}
template <class T> ostream& operator<<(ostream& os, vector<T> v) {
os << "[";
int cnt = 0;
for(auto vv : v) { os << vv; if(++cnt < v.size()) os << ","; }
return os << "]";
}
template <class T> ostream& operator<<(ostream& os, set<T> v) {
os << "[";
int cnt = 0;
for(auto vv : v) { os << vv; if(++cnt < v.size()) os << ","; }
return os << "]";
}
template <class L, class R> ostream& operator<<(ostream& os, pair<L, R> p) { return os << "(" << p.fi << "," << p.se << ")"; }
void debug_out() { cerr << endl; }
template <typename Head, typename... Tail> void debug_out(Head H, Tail... T) { cerr << " " << H, debug_out(T...); }
// ....................................................... //
struct rect {
int s, e, w;
rect(int s = 0, int e = 0, int w = 0) : s(s), e(e), w(w) { }
};
const int MAXN = 1e5+10;
int n, m, tlen, begh, finh, ah[MAXN], aw[MAXN], bh[MAXN], bw[MAXN];
vector<rect> ar;
void input() {
// ---- !!! INIT GLOBAL VARIABLES !!! ---- //
cin >> tlen >> begh >> finh;
cin >> n;
FOR(i, 0, n) cin >> aw[i] >> ah[i]; ah[n] = ah[n-1];
cin >> m;
FOR(i, 0, m) cin >> bw[i] >> bh[i]; bh[m] = bh[m-1];
}
// 직사각형 형태로 만든다.
void generateRec() {
ar.clear();
int ap = 0, bp = 0, x = 0, ax = 0, bx = 0;
while(ap < n || bp < m) {
rect cur;
if(bp == m || (ap < n && ax + aw[ap] < bx + bw[bp])) {
cur = { bh[bp], ah[ap], ax + aw[ap] - x };
x = ax = ax + aw[ap];
++ap;
} else {
cur = { bh[bp], ah[ap], bx + bw[bp] - x };
x = bx = bx + bw[bp];
++bp;
}
if(cur.w != 0) ar.pb(cur);
}
}
// 조건에 맞는 껍질을 { height }로 반환
vector<int> getConvex(vector<rect>& ar, int beg) {
vector<int> ret(ar.size(), 0);
vector<int> minu(ar.size()), maxd(ar.size());
// i에서부터의 상한, 하한을 구한다.
RFOR(i, sz(ar)-1, 0) {
minu[i] = min(i+1 == ar.size() ? 0x7fffffff : minu[i+1], ar[i].e);
maxd[i] = max(i+1 == ar.size() ? -0x7fffffff : maxd[i+1], ar[i].s);
// 현재에서 상한, 하한이 서로를 뛰어 넘는 경우
// 상한이 하한보다 낮아진다면? 하한을 이걸로 조정!
if(ar[i].e < maxd[i]) maxd[i] = ar[i].e;
// 하한이 상한보다 높아진다면? 상한을 이걸로 조정!
if(ar[i].s > minu[i]) minu[i] = ar[i].s;
}
int cur = beg;
FOR(i, 0, ar.size()) {
// 현재 높이보다 낮아질 필요는 없다.
ret[i] = min(cur, ar[i].e);
// 하한보다 낮아질 필요는 없다.
ret[i] = max(ret[i], min(ar[i].e, maxd[i]));
// 상한보다는 낮아야 한다.
ret[i] = max(ret[i], max(ar[i].s, minu[i]));
cur = ret[i];
}
return ret;
}
int solve() {
generateRec();
// 귀찮은거 따로 처리
if(ar.size() == 1) {
cout << (i64)ar[0].w * abs(begh - finh) << ENDL;
return 0;
}
// 위 껍질 찾기
vector<rect> tmp = ar;
tmp.pb({ finh, finh, 0 });
vector<int> up = getConvex(tmp, begh);
debug(up);
// 아래 껍질 찾기
FOR(i, 0, ar.size()) {
ar[i].s = -ar[i].s;
ar[i].e = -ar[i].e;
swap(ar[i].s, ar[i].e);
}
ar.pb({ -finh, -finh, 0 });
vector<int> dw = getConvex(ar, -begh);
debug(dw);
// 계산
i64 ans = 0;
FOR(i, 0, ar.size()-1) {
ans += (i64)ar[i].w * (up[i] + dw[i]);
}
cout << ans << ENDL;
return 0;
}
// ................. main .................. //
void execute() {
#ifdef LOCAL_BOOKNU
auto START_TIME = clock();
#endif
int TTT; cin >> TTT;
FOR(ttt, 0, TTT) cout << "Case #" << ttt+1 << ENDL,
input(), solve();
#ifdef LOCAL_BOOKNU
auto END_TIME = clock();
cout << ENDL << END_TIME - START_TIME << "ms" << ENDL;
#endif
}
int main(void) {
#ifdef LOCAL_BOOKNU
// freopen("input.txt", "r", stdin);
// freopen("out.txt", "w", stdout);
#endif
cin.tie(0), ios_base::sync_with_stdio(false);
execute();
return 0;
}
// ......................................... //
후기
삽질하면서 푸느라 설명도 좀 이상해지고 코드에도 쓸모 없는 부분이 있을 것 같은데, 나중에 더 깔끔한 풀이를 보고 다시 풀어봐야겠다.
4번
휴리스틱 그리디
$50 \times 500$의 맵이 주어지고, 부숴야 할 집들이 주어진다.
하나의 폭탄은 $3 \times 3$범위만을 폭파시킬 수 있을 때, 폭탄을 최소로 사용해 모든 집을 부숴야 한다.
풀이 보기
우선 위의 식을 개념적으로 풀어서 이해하면, 일단 세그먼트 단위로 쪼갠 후, 각 세그먼트에 들어있는 원소들의 합에 세그먼트 idx를 곱한것들의 합을 구하는 것으로 바뀐다. 즉, 현재 맵에서 $3 \times 3$ 범위 중 집이 가장 많이 포함되는 곳을 선택해 폭탄을 사용하는 방식으로 구현했다.
모든 경우에서 최적의 결과가 나오지는 않지만, 그럭저럭 좋은 결과는 나온다.
단, 현재 맵 상태에서 모든 곳에 폭탄을 터뜨려보는 것은 시간초과가 발생할 수 있으므로, 약간 트리키하게 구현했다.
소스코드 보기
#include <bits/stdc++.h>
using namespace std;
#ifdef LOCAL_BOOKNU
#define debug(...) cerr << "[" << #__VA_ARGS__ << "]:", debug_out(__VA_ARGS__)
#else
#define debug(...) 42
#endif
// ........................macro.......................... //
#define FOR(i, f, n) for(int (i) = (f); (i) < (int)(n); ++(i))
#define RFOR(i, f, n) for(int (i) = (f); (i) >= (int)(n); --(i))
#define pb push_back
#define emb emplace_back
#define fi first
#define se second
#define ENDL '\n'
#define sz(A) (int)(A).size()
#define ALL(A) A.begin(), A.end()
#define UNIQUE(c) (c).resize(unique(ALL(c)) - (c).begin())
#define next next9876
#define prev prev1234
typedef pair<int, int> ii;
typedef pair<int, ii> iii;
typedef vector<int> vi;
typedef vector<vi> vvi;
typedef vector<ii> vii;
typedef vector<vii> vvii;
typedef long long i64;
typedef unsigned long long ui64;
// inline i64 GCD(i64 a, i64 b) { if(b == 0) return a; return GCD(b, a % b); }
inline int getidx(const vi& ar, int x) { return lower_bound(ALL(ar), x) - ar.begin(); } // 좌표 압축에 사용: 정렬된 ar에서 x의 idx를 찾음
inline i64 GCD(i64 a, i64 b) { i64 n; if(a < b) swap(a, b); while(b != 0) { n = a % b; a = b; b = n; } return a; }
inline i64 LCM(i64 a, i64 b) { if(a == 0 || b == 0) return GCD(a, b); return a / GCD(a, b) * b; }
inline i64 CEIL(i64 n, i64 d) { return n / d + (i64)(n % d != 0); } // 음수일 때 이상하게 작동할 수 있음.
inline i64 ROUND(i64 n, i64 d) { return n / d + (i64)((n % d) * 2 >= d); }
const i64 MOD = 1e9+7;
inline i64 POW(i64 a, i64 n) {
assert(0 <= n);
i64 ret;
for(ret = 1; n; a = a*a%MOD, n /= 2) { if(n%2) ret = ret*a%MOD; }
return ret;
}
template <class T> ostream& operator<<(ostream& os, vector<T> v) {
os << "[";
int cnt = 0;
for(auto vv : v) { os << vv; if(++cnt < v.size()) os << ","; }
return os << "]";
}
template <class T> ostream& operator<<(ostream& os, set<T> v) {
os << "[";
int cnt = 0;
for(auto vv : v) { os << vv; if(++cnt < v.size()) os << ","; }
return os << "]";
}
template <class L, class R> ostream& operator<<(ostream& os, pair<L, R> p) { return os << "(" << p.fi << "," << p.se << ")"; }
void debug_out() { cerr << endl; }
template <typename Head, typename... Tail> void debug_out(Head H, Tail... T) { cerr << " " << H, debug_out(T...); }
// ....................................................... //
const int MAXN = 510;
int n, m, dp[51][MAXN];
string g[51];
set<iii> lis;
void input() {
// ---- !!! INIT GLOBAL VARIABLES !!! ---- //
cin >> n >> m;
FOR(i, 0, n) cin >> g[i];
}
void eraseBomb(int y, int x) {
for(int dy : {-1, 0, 1}) {
for(int dx : {-1, 0, 1}) {
int ny = y+dy, nx = x+dx;
if(0 < ny && ny < n-1 && 0 < nx && nx < m-1) {
auto it = lis.find({ dp[ny][nx],{ ny, nx } });
if(it != lis.end()) {
dp[ny][nx] = it->first + 1;
lis.erase(it);
lis.insert({ dp[ny][nx], {ny, nx} });
}
}
}
}
}
int solve() {
lis.clear();
memset(dp, 0, sizeof(dp));
FOR(i, 1, n-1) {
FOR(j, 1, m-1) {
int cc = 0;
for(int dy : { -1, 0, 1 }) {
for(int dx : { -1, 0, 1 }) {
int ny = i + dy, nx = j + dx;
if(g[ny][nx] == '1') {
++cc;
}
}
}
lis.insert({ -cc, { i, j } });
dp[i][j] = -cc;
}
}
int rem = 0;
FOR(i, 0, n) FOR(j, 0, m) if(g[i][j] == '1') ++rem;
vii ans;
while(rem) {
iii cur = *lis.begin();
lis.erase(lis.begin());
int cc = -cur.fi, cy = cur.se.fi, cx = cur.se.se;
rem -= cc;
ans.pb({ cy, cx });
for(int dy : {-1, 0, 1}) {
for(int dx : { -1, 0, 1}) {
int y = cy+dy, x = cx+dx;
if(g[y][x] == '1') {
eraseBomb(y, x);
g[y][x] = '0';
}
}
}
}
cout << ans.size() << ENDL;
FOR(i, 0, ans.size()) cout << ans[i].fi << ' ' << ans[i].se << ENDL;
return 0;
}
// ................. main .................. //
void execute() {
#ifdef LOCAL_BOOKNU
auto START_TIME = clock();
#endif
int TTT; cin >> TTT;
FOR(ttt, 0, TTT) cout << "Case #" << ttt+1 << ENDL,
input(), solve();
#ifdef LOCAL_BOOKNU
auto END_TIME = clock();
cout << ENDL << END_TIME - START_TIME << "ms" << ENDL;
#endif
}
int main(void) {
#ifdef LOCAL_BOOKNU
// freopen("input.txt", "r", stdin);
// freopen("out.txt", "w", stdout);
#endif
cin.tie(0), ios_base::sync_with_stdio(false);
execute();
return 0;
}
// ......................................... //
후기
어차피 만점 못 받을거 긁어보기나 하자 해서 구현해봤는데, 만점이 나와서 놀랐다.
다른 분들 얘기를 들어보면 테케가 좋지 못했던 것 같다.
5번
풀지는 못했지만, $5 \cdot 10^4$ 입력 범위는 해결할 수 있는 방법이 떠올라서 적는다. (정상적으로 동작하는지는 확인하지 못했다.)
기본 아이디어는 간단한데, 각 점의 우상에 있는 점들 중 $max(xdis, ydis)$가 가장 작은 것을 사각형의 변으로 하면 된다.
그러나 점이 많기 때문에, 단순한 방법으로는 $O(n^2)$의 시간이 걸린다.
이분 탐색 아이디어를 사용하면 $O(n \cdot \log^3n)$의 시간에 해결할 수 있다.
각 점에서 “길이가 $x$인 사각형을 사용할 수 있나?” 를 판단하는 함수를 평면에서 범위에 속하는 점의 수를 $O(\log^2n)$에 셀 수 있는 2D segtree를 이용하여 구현하고, 이를 통해 이분 탐색을 하면 $5 \cdot 10^4$ 범위에서는 해결이 가능하다.
더 좋은 방법은 다른 방법으로 접근해야 할 것 같다.
후기
- 3번이 아이디어를 떠올리기 어렵고, 구현도 까다로워서 힘들었다.
- 4번은 긁어나 보자는 심정으로 구현했는데, 만점이 떠서 운이 좋았던 것 같다.
- 5번은 섭테 2번까지는 긁을 수 있을 것 같았지만, 섭테 1도 제대로 동작하지 않아서 던지고 밥이나 먹으러 갔다