문제
BOJ 15584(https://www.acmicpc.net/problem/15584)
$n$개의 정점을 가진 트리가 있다.
Bessie는 임의의 정점에서 시작하여 아무 $leaf$를 통해 탈출하려고 하고, 농부들은 여러 $leaf$에서 시작하여 Bessie가 leaf에 도달하기 전에 붙잡으려고 한다.
Bessie와 농부는 같은 이동속도를 가지고 있으며, 따라서 Bessie는 정점에서 붙잡히거나 간선을 건너는 도중 붙잡힐 수 있다.
Bessie와 농부는 항상 최선의 수로 움직인다고 하고, 각 정점마다 Bessie가 해당 정점에서 출발할 때 절때 leaf에 도달하지 못하도록 하기 위해 배치해야 할 농부의 최소 수를 구해야 한다.
(Bessie가 leaf에서 시작하는 경우에 대해서도 구해야하며, 이 때는 해당 $leaf$에 농부가 있으면 붙잡을 수 있다.)
문제 분석
Bessie의 위치가 고정되어 있을 경우
분석을 위해, 시작 위치가 고정된 경우에 대해서만 생각해보자
(이 경우는 USACO Gold 버전으로 나와있다. Cow at Large (Gold))
Bessie와 하나의 농부와의 관계
우선 Bessie의 시작점과, 한 농부의 시작점에 대해서만 고민해보자.
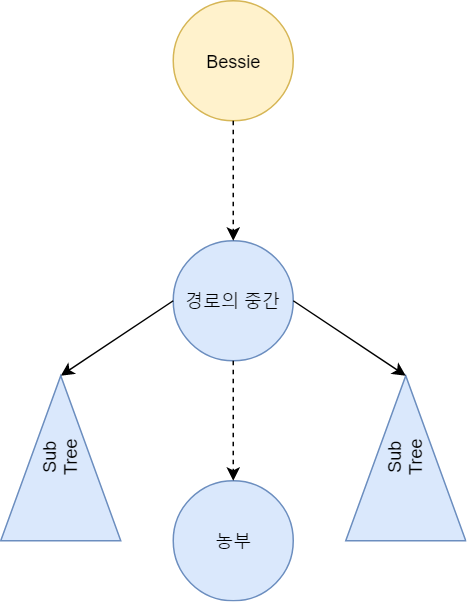
트리 구조에 의해 둘 사이에는 유일한 경로가 존재할 것이며, 해당 농부가 존재하므로써 Bessie는 농부로부터 시작하여 경로의 중간까지의 경로에 존재하는 모든 정점을 포함한 $subtree$로 갈 수 없게 된다.
즉, 아래 그림과 같이 파란색인 곳은 갈 수 없게 되는 것이다.
그리디하게 leaf를 선택하는 방법
그럼 Bessie의 시작 위치가 고정되어있다(편의상 $root$라고 하자)고 할 때, $leaf$는 어떤 순서로 골라야할까?
잘 관찰해보면 $root$와 가장 가까운 $leaf$들부터 선택하는 것이 무조건 이득이라는 것을 알 수 있다.
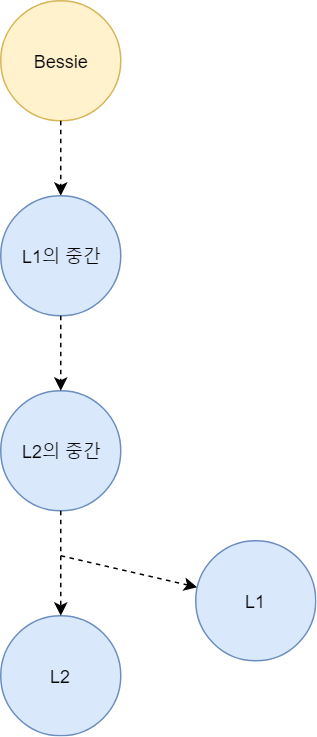
간단하게 증명하면, $dist(root, l_1) < dist(root, l_2)$인 두 $leaf$ $l_1, l_2$가 있다고 할 때, $l_2$를 먼저 선택하여 $l_1$을 선택하는 것보다 더 이득을 보는 경우가 있을까?
- $path(l_1의\ 중간, l_1)$과 $path(l_2의\ 중간, l_2)$가 겹치는 정점이 없다.
- 이 경우에는 어차피 $l_1, l_2$를 제외하기 위해 $leaf$들을 골라야하므로 상관이 없다.
- 즉, $l_1, l_2$를 선택하므로서 제외되는 부분들이 완전히 다르기 때문에 뭘 선택하든 상관없다.
- 겹치는 정점이 있다.
- 이 경우, 무조건 $l_1$을 선택하는게 이득인데, $l_1의\ 중간$정점이 항상 $l_2의\ 중간$정점보다 같거나 $root$와 가깝기 때문이다.
- 즉, 아래 그림과 같은 관계가 된다.
효율적으로 가장 가까운 leaf들을 고르는 방법
일단 가까운 $leaf$들을 고른다는건 알겠는데, Naive하게 $leaf$를 고르고 정점들을 제외하고를 반복하는건 너무 비효율적이다.
$leaf$가 선택되어 그 $subtree$들이 제외되는 과정을 살펴보면, $subtree$의 $root$는 결국 $path(root, leaf)$의 중간 정점이라는 것을 알 수 있다.
각 정점마다 root로부터의 거리($=d_{root}[u]$), 해당 leaf로부터의 거리($=d_{leaf}[u]$)를 계산해놓았다고 가정했을 때, 결국 $leaf$를 고름으로써 제외되는 $subtree$의 $root$는 정점들 중 $d_{leaf}[u] <= d_{root}[u] \land d_{leaf}[par] > d_{root}[par]$ 인 $u$라는 것을 알 수 있다.
또한, $subtree$가 다른 $subtree$에 포함되는 경우 해당 $leaf$를 선택하지 않아도 알아서 제외되므로, $u$에서 가장 가까운 leaf까지의 거리($=d_{leaf}[u]$)만을 고려하여 인 정점$d_{leaf}[u] <= d_{root}[u] \land d_{leaf}[par] > d_{root}[par]$들의 수를 세기만 하면 된다.
(결국 가장 가까운 $leaf$들부터 고르는 효과를 얻게 된다.)
(또한 $d_{leaf}[u]$가 $root$를 지나서 있는 $leaf$에 대해서 계산된다고 해도 문제가 될게 없다.)
Bessie가 모든 위치에서 등장하는 경우
하지만 위 방법의 결정적인 단점은, 트리의 $root$가 바뀐 경우 $d_{root}$를 다시 계산해야하고, 그에 따라 답을 구하기 위해 다시 모든 정점을 순회해야한다는 것에 있다.
수학적으로 답을 구하자
사실 $root$가 고정되어 있고, $d_{root}, d_{leaf}$가 계산되어 있을 때 수학적으로 답을 구하는 방법이 있다.
결국은 트리에서 생기는 $subtree$의 개수를 세는게 문제인데, 하나의 $subtree$에 집중해서 보면 재미있는 사실을 알 수 있다.
트리의 정점의 수가 $k$개라고 할 때 간선의 수는 $k-1$개이고, 따라서 모든 정점의 차수의 합은 $2 k -2$가 된다.
단, $subtree$에서는 무조건 $subtree$의 $root$로 오는 간선이 하나 존재하기 때문에 전체 트리의 측면에서 봤을 때 차수의 합은 $2k-1$이 된다.
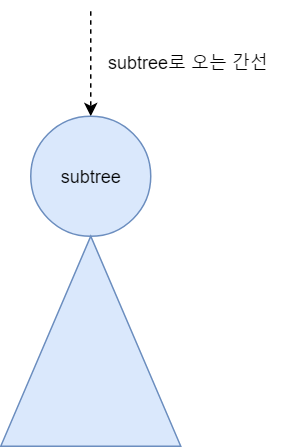
즉, $\sum\limits_{u \in subtree}deg(u) = 2k-1$이고,$\sum\limits_{u \in subtree}2-deg(u) = 1$이 된다.
이것을 통해 단순히 어떤 $subtree$에든 속할 수 있는 정점들을 모아 $\sum{2-deg(u)}$를 구한다면 그게 바로 답이 되는 것이다.
$u$가 어떤 $subtree$에 속할 수 있는 조건은 위에서 명시한 $d_{leaf}[u] <= d_{root}[u]$를 만족시키는 것들이 이에 속한다.
($d_{leaf}[par] > d_{root}[par]$이라는 조건은 $u$가 $subtree$의 $root$일 때 붙는다.)
$d_{leaf}[u] - d_{root}[u] <= 0$인 정점들에 대해서 $2-deg(u)$의 합을 구하면 되므로, Fenwick Tree를 쓰기 적합하다.
($dif[u] = d_{leaf}[u] - d_{root}[u]$를 index로 사용하고, $2-deg(u)$를 value로 사용하여 $[..0]$까지의 합을 구하면 된다.)
$root$가 변경 될 때 $dif[u]$의 변화
$root$가 자식으로 변경되었을 때($root_{prev} \rightarrow root_{cur}$)를 생각해보면, $root_{cur}$을 포함하는 $subtree$의 $dif[u]$는 전부 $1$씩 증가하고, 그 외의 정점들의 경우 $1$씩 감소한다는 것을 알 수 있다.
($dif[u]$는 $d_{root}[u]$에만 영향을 받기 때문에)
위의 경우를 위한 자료구조
이에 따라 Fenwick Tree에서 $root_{cur}$의 $subtree$부분은 index를 전부 1씩 증가시켜야하고, 나머지는 index를 1씩 감소시켜야 하는데, 이것을 원소마다 일일이 옮긴다면 굉장히 비효율적일 것이다.
범위에 대한 조작이 가능한 Lazy Propagation을 생각해보면 이것은 구간에 일정한 value를 조작할 때 느긋한 전파를 이용해 성능을 높이는 방법인데, 이 경우는 index 자체를 한꺼번에 옮기는 연산을 구현하기에는 적합하지 않다.
정점의 수가 $7 \cdot 10^4$으로 꽤나 적다는 것을 이용하여 정점들을 $\sqrt{n}$개의 각각 $\sqrt{n}$개의 정점을 포함하는 Fenwick Tree로 쪼개어서 저장하면 일정 범위를 이동시키는 연산을 양 끝에 포함되는 두 Fenwick Tree에 대해서는 일일이 원소들을 옮겨주고, 중간에 존재하는 Fenwick Tree들에 대해서는 일정한 index를 옮겼다는 $lazy$표시를 해두는 방식으로 구현하면 $O(\sqrt{n} \cdot \log{n})$의 시간복잡도를 가지게 된다.
트리에서 $\sqrt{n}$개씩 정점들을 묶기에 좋은 방법은 inorder방식으로 정점들에 번호를 매겨서 묶는 것이다.
inorder의 좋은 점은 $u$의 $subtree$ 정점들은 모두 연속된 번호를 부여받게 되어 $subtree$의 모든 정점들에 대해서 다뤄야 하는 이 문제에서 쓰기에 아주 적합하다.
종합
결론적으로 총체적인 알고리즘 흐름을 보자면
- 임의의 정점을 $root$로 삼고 그에 대한 $dif[u]$들을 구해놓자.
inorder을 통해 정점에 번호를 부여하고, 그것들을 $\sqrt{n}$개씩 묶어서 각 범위마다Fenwick Tree를 만들어놓자.Fenwick Tree에는 $dif[u]$를 index로, $2-deg(u)$를 value로 값들을 넣어놓고 답을 구할 때 index = $[,0]$인 value들의 합을 구하자.dfs를 통해서 답을 구해가는데, $root$를 $child$로 옮길 때는 그 $subtree$에는 $dif[u]$들을 전부 $1$씩 더하고, 나머지에는 $-1$씩 더하자- 이것은
Fenwick Tree에서 index를 옮기는 작업이므로, $subtree$에 $1$을 더하는 경우를 살펴보면 구간이 여러Fenwick Tree로 구성되어 있다면 양 끝 구간에는 일일이 index를 옮겨주고, 중간 구간에는 $lazy$를 통해 옮겼다는 표시만을 남기자.
- 이것은
- 이 때, $leaf$자체가 $root$가 되는 경우는 알고리즘이 이상하게 작동되므로, 예외처리를 해주자.
소스코드
#include <bits/stdc++.h>
using namespace std;
#ifdef LOCAL_BOOKNU
#define debug(...) cerr << "[" << #__VA_ARGS__ << "]:", debug_out(__VA_ARGS__)
#else
#define debug(...) 42
#endif
// ........................macro.......................... //
#define FOR(i, f, n) for(int (i) = (f); (i) < (int)(n); ++(i))
#define RFOR(i, f, n) for(int (i) = (f); (i) >= (int)(n); --(i))
#define pb push_back
#define emb emplace_back
#define fi first
#define se second
#define ENDL '\n'
#define sz(A) (int)(A).size()
#define ALL(A) A.begin(), A.end()
#define UNIQUE(c) (c).resize(unique(ALL(c)) - (c).begin())
#define next next9876
#define prev prev1234
typedef pair<int, int> ii;
typedef pair<int, ii> iii;
typedef vector<int> vi;
typedef vector<vi> vvi;
typedef vector<ii> vii;
typedef vector<vii> vvii;
typedef long long i64;
typedef unsigned long long ui64;
// inline i64 GCD(i64 a, i64 b) { if(b == 0) return a; return GCD(b, a % b); }
inline int getidx(const vi& ar, int x) { return lower_bound(ALL(ar), x) - ar.begin(); } // 좌표 압축에 사용: 정렬된 ar에서 x의 idx를 찾음
inline i64 GCD(i64 a, i64 b) { i64 n; if(a < b) swap(a, b); while(b != 0) { n = a % b; a = b; b = n; } return a; }
inline i64 LCM(i64 a, i64 b) { if(a == 0 || b == 0) return GCD(a, b); return a / GCD(a, b) * b; }
inline i64 CEIL(i64 n, i64 d) { return n / d + (i64)(n % d != 0); } // 음수일 때 이상하게 작동할 수 있음.
inline i64 ROUND(i64 n, i64 d) { return n / d + (i64)((n % d) * 2 >= d); }
const i64 MOD = 1e9+7;
inline i64 POW(i64 a, i64 n) {
assert(0 <= n);
i64 ret;
for(ret = 1; n; a = a*a%MOD, n /= 2) { if(n%2) ret = ret*a%MOD; }
return ret;
}
template <class T> ostream& operator<<(ostream& os, vector<T> v) {
os << "[";
int cnt = 0;
for(auto vv : v) { os << vv; if(++cnt < v.size()) os << ","; }
return os << "]";
}
template <class T> ostream& operator<<(ostream& os, set<T> v) {
os << "[";
int cnt = 0;
for(auto vv : v) { os << vv; if(++cnt < v.size()) os << ","; }
return os << "]";
}
template <class L, class R> ostream& operator<<(ostream& os, pair<L, R> p) { return os << "(" << p.fi << "," << p.se << ")"; }
void debug_out() { cerr << endl; }
template <typename Head, typename... Tail> void debug_out(Head H, Tail... T) { cerr << " " << H, debug_out(T...); }
// ....................................................... //
struct fenwick {
int n;
vi t;
void init(int _n) {
n = _n;
t.assign(n+1, 0);
}
void add(int u, int x) {
for(++u; u <= n; u += (u&-u)) t[u] += x;
}
int sum(int u) {
int ret = 0;
for(++u; u > 0; u -= (u&-u)) ret += t[u];
return ret;
}
};
const int RN = 265, MAXN = RN*RN;
// dr, dl : 현재 정점부터 root까지, 최단 leaf까지 거리
// sn, en : inorder 순으로 정점에 번호를 부여할 때, u의 subtree의 번호 범위
// lza : 모든 노드에 더해진 dif, lz[b] : b번째 블럭 전체에 더해진 dif, dif[u] : u정점 자체에 더해진 dif
int n, dr[MAXN], dl[MAXN], deg[MAXN], ans[MAXN], sn[MAXN], en[MAXN], lza, lz[RN], dif[MAXN];
vi g[MAXN];
// dif : 0의 기준을 MAXN으로 사용한다.
// idx = dif, val = w = 2-deg(u)
fenwick ft[RN];
void input() {
cin >> n;
FOR(i, 1, n) {
int u, v; cin >> u >> v; --u, --v;
g[u].pb(v);
g[v].pb(u);
}
}
// dr, dl 계산
void disDfs(int u, int d, int p) {
dr[u] = d;
if(g[u].size() == 1) dl[u] = 0;
else dl[u] = 0x7fffffff;
for(int v : g[u]) {
if(v == p) continue;
disDfs(v, d+1, u);
dl[u] = min(dl[u], dl[v] + 1);
}
}
// dl[u] : u의 부모로부터 오는 leaf도 생각
void disDfs2(int u, int p) {
if(p != -1) dl[u] = min(dl[u], dl[p] + 1);
for(int v : g[u]) {
if(v == p) continue;
disDfs2(v, u);
}
}
// sn, en 계산
int inorder(int u, int c, int p) {
sn[u] = c;
for(int v : g[u]) {
if(v == p) continue;
c = inorder(v, c+1, u);
}
return en[u] = c;
}
// 블럭 b에서 일부 [s, e] 정점들의 dif에 x를 더해준다.
// s, e는 inorder에 의해 부여된 정점 번호들이다.
void updateBlock(int b, int s, int e, int x) {
FOR(i, s, e+1) ft[b].add(dif[i], -deg[i]);
FOR(i, s, e+1) ft[b].add(dif[i] += x, deg[i]);
}
// u의 subtree의 dif에 전부 x를 더한다.
void updateSubtree(int u, int x) {
int sb = sn[u]/RN, eb = en[u]/RN;
// 한 블럭안에 다 들어가는 경우 따로 처리
if(sb == eb) {
updateBlock(sb, sn[u], en[u], x);
return;
}
// 첫, 끝 블록은 쪼개어지기 때문에 따로 직접 처리한다.
updateBlock(sb, sn[u], (sb+1)*RN-1, x);
updateBlock(eb, eb*RN, en[u], x);
// 중간 블록들은 블록 단위로 lazy를 적용한다.
FOR(i, sb+1, eb) lz[i] += x;
}
// dfs로 답을 채워간다.
void getans(int u, int p) {
// 현재 u를 기준으로 답을 구한다.
// dif <= 0인 w들의 합 = subtree의 개수
i64 res = 0;
for(int i = 0; i < RN; ++i) {
res += ft[i].sum(MAXN - lz[i] - lza); // 현재 dif + lz + lza인 값이 dif에 들어있으므로, MAXN - lz[i] - lza까지의 합을 구해야 0까지의 합을 구할 수 있음.
}
ans[u] = res;
// 재귀
for(int v : g[u]) {
if(v == p) continue;
// dif 조절 : subtree에는 ++dif, 그 외에는 --dif
--lza;
updateSubtree(v, 2);
getans(v, u);
// 복구
++lza;
updateSubtree(v, -2);
}
}
int solve() {
FOR(i, 0, RN) ft[i].init(2*MAXN);
disDfs(0, 0, -1);
disDfs2(0, -1);
inorder(0, 0, -1);
// 0-rooted일 경우 초기 계산.
FOR(i, 0, n) {
dif[sn[i]] = dl[i]-dr[i]+MAXN;
deg[sn[i]] = 2-(int)g[i].size();
ft[sn[i]/RN].add(dif[sn[i]], deg[sn[i]]);
}
getans(0, -1);
FOR(i, 0, n) cout << (g[i].size() == 1 ? 1 : ans[i]) << ENDL;
return 0;
}
// ................. main .................. //
void execute() {
input(), solve();
}
int main(void) {
#ifdef LOCAL_BOOKNU
freopen("input.txt", "r", stdin);
freopen("out.txt", "w", stdout);
#endif
cin.tie(0), ios_base::sync_with_stdio(false);
execute();
return 0;
}
// ......................................... //
후기
이번 문제는 해설을 봐도 이해하는데 한참이 걸렸다.
그만큼 해설에서 함축된 지식을 많이 알아야하기 때문에 어려운 문제였던 것 같다.
내가 해설을 보기 전 문제를 분석했을 때 알아낸 것은
- 가장 가까운 $leaf$들을 먼저 고르는게 무조건 이득
- 결국은 고른 $leaf$들에 의해 제외되는 정점들을 그려보면 어떠한 $subtree$형태로 나옴
이 정도인데, $root$와 $shortest\ leaf$의 거리를 이용해 정점들을 선택하고, 차수를 이용해 쉽게 정답을 구하는 방법을 생각하지 못해 못 풀었던것 같다.
이번 문제와 같이 수학적으로 우아하게 식을 세워보는게 추상적으로 생각하는 것보다 훨씬 문제풀이에 도움이 된다는 것을 알았으니 다음부터는 최대한 수학적인 식을 세워보도록 노력해야겠디.