문제
BOJ 2803(https://www.acmicpc.net/problem/2803)
$n$개의 $m$종류의 장난감이 들어갈 수 있는 상자가 있다.
각 상자에는 $m$종류 중 일부의 장난감만이 들어 있을 때,
모든 종류의 장난감을 얻을 수 있도록 상자를 선택하는 방법의 수는?
문제 분석
즉, 집합에 $n$개의 $m$-bit 숫자들이 원소로 있을 때,
부분 집합의 원소들의 or 연산 결과가 $m$-bit의 $1111…$이 되는 경우의 수를 세는 문제이다.
DP 아이디어
다음과 같은 DP 식을 사용하면, $O(n \cdot 2^m)$ 시간복잡도로 해결 할 수 있다.
$dp[i][mask] = 현재$ $i$까지 고려했을 때, $mask$ 상태가 되는 경우의 수
하지만, 이렇게 구현하면 시간초과가 날 것이 분명하니, 다른 방법을 생각해야 한다.
분할정복 아이디어
편하게 submask가 되는 방법들을 생각해보자
정확히 $mask$가 되는 경우를 생각하지 말고, $mask$의 $submask$가 되는 경우를 생각하는 것이 더 편할 것이다.
따라서
$b[x] = 수들$ 중 $x$의 서브마스크가 되는 경우의 수
$c[x] = 수들$의 or 결과가$x$의 서브마스크가 되는 경우의 수
$c[x] = 2^{b[x]}$로 구하면 되니까, $b[x]$를 구하는 방법에 대해서만 생각하면 된다.
또한 어찌됐건 or의 결과가 정확히 $x$가 되는 경우도 구해야 하니까, 이것을 $a[x]$라고 하자.
분할정복으로 $b[x]$ 구하기
우선 $b[x]$에는 초기의 $x$자체인 숫자의 수를 넣어주고, 분할정복을 통해 이것을 우리가 원하는 $b[x]$(OR 결과가 $x$의 submask가 되는 경우의 수)로 만들 것이다.
이 때, 이 과정을 각 bit를 순회하며 $b[x의\ ith{-}bit가\ 켜진\ 경우]$에 $b[x의\ ith{-}bit가\ 꺼진\ 경우]$를 더해가는 방법을 사용 할 것인데, 이것을 구현하기 위해 분할정복을 사용 할 것이다.
즉, 다음과 같이 $[0, 2^m)$구간을 분할정복하며 위의 방법을 사용할 것이다.
(다음 그림은 $m = 3$인 경우이다.)
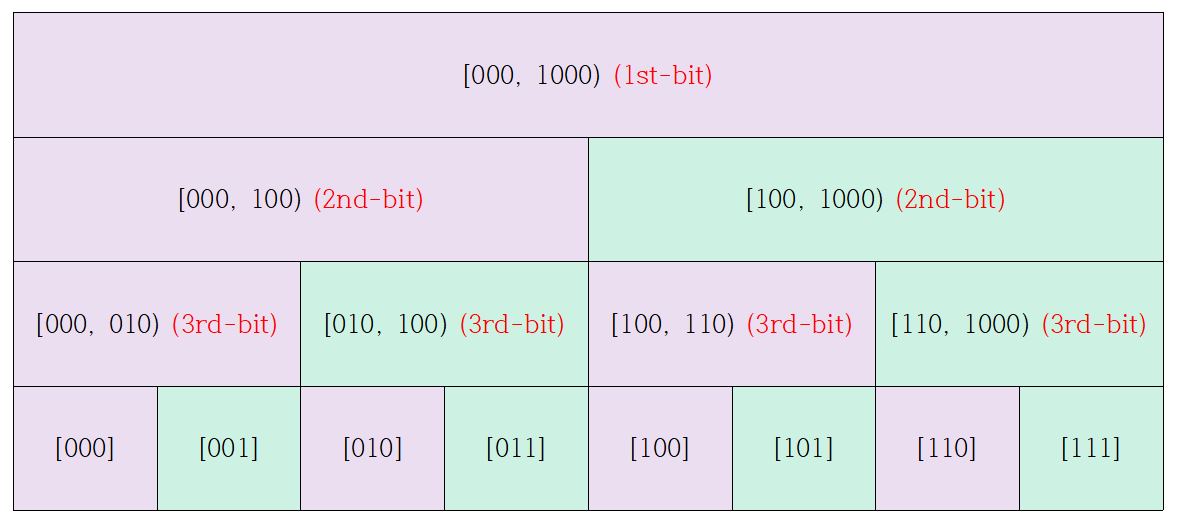
가장 상위 구간 $[000, 1000)$에서는 $1st{-}bit$가 켜진 경우에 그것이 꺼진 경우를 더할 것이고, 아래에서도 재귀적으로 그것을 적용할 것이다.
(즉, 구간을 반으로 쪼개면 $[000, 100), [100, 1000)$이 되는데, 왼쪽 구간의 값을 오른쪽 구간에 더하는 것이다.)
이것이 가능한 이유는 총 구간이 $2^m$(2의 제곱수) 형태이기 때문에, 분할정복을 할 시 각 레벨의 길이는 항상 $2^{m-lv}$이 되고, 그 레벨을 반으로 쪼갤 경우 항상 $(lv+1)$-bit가 켜지고 꺼진 경우로 나눌 수 있기 때문이다.
이렇게 재귀의 끝까지 가면 항상 $b[x]$가 우리가 원하던 “$x$의 $submask$인 수의 수”가 됨을 보장 할 수 있다.
그 이유는 우선 최상위 레벨에서는 $b[x]$가 $1st{-}bit$이 켜지고 꺼진 경우를 포함하게 되고, 다음 레벨에서는 위의 결과를 이어받고, $b[x]$가 $(1,2)th{-}bit$가 켜지고 꺼진 경우를 포함하게 되고, 이를 재귀적으로 반복하면 결국 재귀의 끝에서는 $b[x]$가 $(1..m)th{-}bit$가 켜지고 꺼진 경우를 모두 포함하게 되는데, 이것이 즉 $x$의 $submask$가 되는 경우를 모두 포함한다는 것이다.
결과적으로는 top-down 방식으로 재귀를 하며 $b[x]$를 구해가는 것이다.
$c[x]$, a[x] 구하기
$c[x] = 2^{b[x]}$로 간단하게 구할 수 있다.
그렇다면 정확히 or 결과가 $x$가 되는 $a[x]$는 어떻게 구할까?
이것 역시 위에서 $b[x]$를 구한 방법과 비슷하게 구할 수 있다.
즉, $c[x의\ ith{-}bit가\ 켜진\ 경우]$에서 $c[x의\ ith{-}bit가\ 꺼진\ 경우]$를 점점 빼가면 결국은 $a[x]$가 된다는 것을 같은 논리로 설명 할 수 있다.
소스코드
구현에서는 직접 a[x], b[x], c[x]를 사용하지 않고 하나의 ar[x]를 사용해서 그것들을 동시에 표현했는데, 이것에 유의하여 보길 바란다.
#ifndef ONLINE_JUDGE
#define _CRT_SECURE_NO_WARNINGS
#endif
#include <bits/stdc++.h>
using namespace std;
// ........................macro.......................... //
// [i, n)
#define FOR(i, f, n) for(int (i) = (f); (i) < (int)(n); ++(i))
// [i, n]
#define RFOR(i, f, n) for(int (i) = (f); (i) >= (int)(n); --(i))
#define pb push_back
#define emb emplace_back
#define fi first
#define se second
#define ENDL '\n'
#define sz(A) (int)(A).size()
#define ALL(A) A.begin(), A.end()
#define UNIQUE(c) (c).resize(unique(ALL(c)) - (c).begin())
#define next next9876
#define prev prev1234
typedef vector<int> vi;
typedef vector<vector<int> > vvi;
typedef vector<pair<int, int> > vii;
typedef vector<vector<pair<int, int> > > vvii;
typedef pair<int, int> ii;
typedef pair<int, pair<int, int> > iii;
typedef long long i64;
typedef unsigned long long ui64;
// inline i64 GCD(i64 a, i64 b) { if(b == 0) return a; return GCD(b, a % b); }
inline int getidx(const vi& ar, int x) { return lower_bound(ALL(ar), x) - ar.begin(); } // 좌표 압축에 사용: 정렬된 ar에서 x의 idx를 찾음
inline i64 GCD(i64 a, i64 b) { i64 n; if(a<b) swap(a, b); while(b!=0) { n = a%b; a = b; b = n; } return a; }
inline i64 LCM(i64 a, i64 b) { if(a == 0 || b == 0) return GCD(a, b); return a / GCD(a, b) * b; }
inline i64 CEIL(i64 n, i64 d) { return n / d + (i64)(n % d != 0); }
inline i64 ROUND(i64 n, i64 d) { return n / d + (i64)((n % d)*2 >= d); }
const i64 MOD = 1e9+7;
inline i64 POW(i64 a, i64 n) {
if(n < 0) return 0;
i64 ret = 1;
while(n) { if(n % 2) ret *= a, ret %= MOD; a = a * a, a %= MOD; n /= 2; }
return ret;
}
void debug_out() { cerr << endl; }
template <typename Head, typename... Tail>
void debug_out(Head H, Tail... T) {
cerr << " " << to_string(H);
debug_out(T...);
}
#ifndef ONLINE_JUDGE
#define debug(...) cerr << "[" << #__VA_ARGS__ << "]:", debug_out(__VA_ARGS__)
#else
#define debug(...) 42
#endif
// ....................................................... //
const int MAXN = 1e6, MAXM = 20;
int n, m;
i64 ar[1<<MAXM];
void input() {
cin >> n >> m;
FOR(i, 0, n) {
int nn, k = 0; cin >> nn;
while(nn--) {
int x; cin >> x; --x;
k |= (1 << x);
}
++ar[k]; // ar[x]의 초기 값: x인 수들의 개수
}
}
// 분할 정복은 구간이 정확히 2의 제곱수가 되게 수행한다.
// 이렇게 함으로써, 왼쪽과 오른쪽 구간의 차이는 정확히 2^(len-1) 만큼 난다.
// 즉, 오른쪽 구간의 수들은 왼쪽 구간의 수들에서 (len-1) bit만 켠 것과 같다.
// 또한 재귀 중 ar[x]가 의미하는 바가 달라진다!
// top-down 재귀가 끝나고 난 바로 뒤의 ar[x] = b[x]
// leaf에서 작업이 끝나고 난 바로 뒤의 ar[x] = c[x]
// 모든 과정이 끝나고 난 뒤의 ar[x] = a[x]
void f(int s, int e) {
// leaf: top-down 재귀의 끝 (c[x] = 2^b[x])
// 이 시점에 ar[x] = b[x]이다.
if(s+1 == e) {
ar[s] = POW(2, ar[s]);
return;
}
// top-down 재귀로 b[x]를 구해나간다.
int m = (s+e)/2;
FOR(i, m, e) ar[i] += ar[s+i-m];
f(s, m), f(m, e);
// top-down 재귀 끝나고 a[x]를 구하는 과정
FOR(i, m, e) {
ar[i] -= ar[s+i-m];
if(ar[i] < 0) ar[i] += MOD;
}
}
int solve() {
f(0, 1 << MAXM);
cout << ar[(1 << m) - 1] << ENDL;
return 0;
}
// ................. main .................. //
void execute() {
input(), solve();
}
int main(void) {
#ifndef ONLINE_JUDGE
freopen("in.txt", "r", stdin);
// freopen("out.txt", "w", stdout);
#endif
cin.tie(0); ios_base::sync_with_stdio(false);
execute();
return 0;
}
// ......................................... //