정렬되지 않은 배열에서 $k$번째 원소를 찾는 문제는 정렬 한 후 배열의 $k$번째 원소가 답이 되기 때문에 정렬 문제보다 쉬운 문제이다.
이 말은 즉, $k$번째 원소 찾기 알고리즘은 최소한 $O(n\log{n})$ 만에 풀 수 있다는 뜻이다.
그러나 Quick Sort의 아이디어를 사용하면 이것을 $O(n)$로 줄일 수 있다.
Quick Sort 활용
Quick Sort는 임의의 $pivot$을 뽑아 투 포인터 형식으로 현재 구간의 양쪽 끝에서 시작한 포인터를 이동시키면서 왼쪽의 $x > pivot$인 원소와 오른쪽의 $y < pivot$인 원소를 swap해가며 구간을 $pivot$보다 작거나 같은 것과 큰 것으로 나누어 나눠진 두 구간에 대해 재귀적으로 이 과정을 적용하는 방식으로 작동한다.
이 때, 우리는 한 가지 생각을 할 수 있다.
$pivot$으로 인해 나눠진 두 구간 중 하나는 아예 재귀를 하지 않아도 되지 않을까?
왜냐하면
- $pivot = k$ : $pivot$의 왼쪽에는 모두 $pivot$보다 작거나 같은 원소가 있고, 오른쪽에는 모두 $pivot$보다 큰 원소가 있으니 $k$번째 원소를 찾은 것이다.
- $pivot < k$ : 똑같은 논리로 $pivot$을 포함한 왼쪽 구간은 확인 할 필요가 없다.
- $pivot > k$ : 역시 $pivot$을 포함한 오른쪽 구간은 확인 할 필요가 없다.
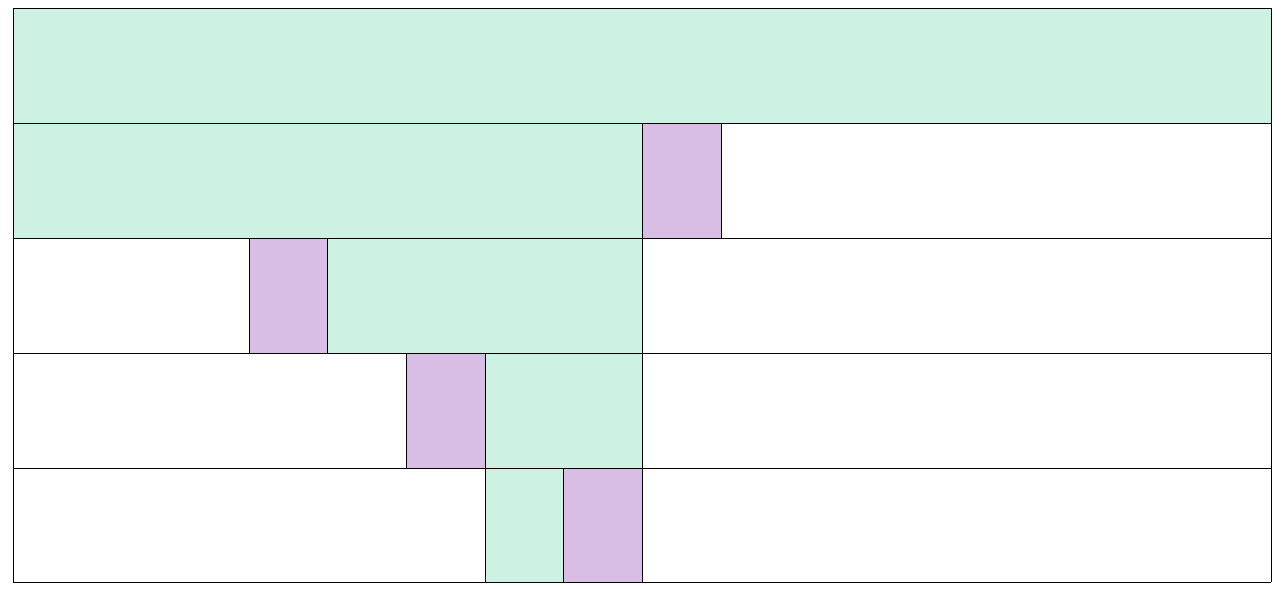
즉, 아래의 그림처럼 연두색 구간에 대해서만 확인을 하면 된다.
(보라색은 그 단계에서의 $pivot$이다.)
($pivot$의 왼쪽은 모두 $pivot$의 이하이고, 오른쪽은 모두 $pivot$의 초과임을 유의하자)
시간복잡도
$pivot$을 아주 잘 잡아서 위의 그림과 같이 이상적으로 구간을 반으로 나눈다고 생각해보자.
그럼 총 시간복잡도는 다음과 같이 선형적으로 된다.
그러나 피벗을 현재 구간의 가장 첫 번째와 같이 최악의 경우로 잡으면, $k=n-1$일 때 시간복잡도가 $O(n^2)$이 된다.
따라서 Quick Sort의 경우와 마찬가지로 $pivot$을 잘 잡는 것이 중요하다.
다행히도 C++ STL에서는 이런 기능을 nth_element 함수로 구현해놓았다.
안정적인 알고리즘
항상 $O(n)$을 보장하는 알고리즘으로는 Median of medians 기법을 활용하는 Intro Select가 있다.
소스코드
// k는 0-idx로 가정한다.
int n, ar[MAXN];
int qselect(int k) {
assert(k < n);
int s = 0, e = n-1;
while(1) {
// pivot = ar[s] (원래는 랜덤하게 뽑아야 하지만, 간단하게 구현하기 위해)
int i = s, j = e;
while(1) {
while(i <= e && ar[i] <= ar[s]) ++i;
while(ar[j] > ar[s]) --j;
if(i >= j) break;
swap(ar[i], ar[j]);
}
swap(ar[s], ar[j]);
// k번째 찾음
if(j == k) return ar[j];
// 구간 조절
else if(j < k) s = j+1;
else e = j-1;
}
}